^_^

牛客基础训练营5B

dyh 发布于 2020-02-14 收录于 Nowcoder

题目在这

这道题可以用二分法，三分法更好一点（反正当时完全没想到），0.618法应该最快

三分是中间的两个点 mid = l + (r - l) / 2 midmid = mid + (r - mid) / 2

Graph Theory

dyh 发布于 2020-02-05 收录于 Algorithm

图的存储：邻接表、邻接矩阵、前向星、链式前向星等

链式前向星存图

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


struct edge{
	int to , w , next;
}e[maxn];
int tot,head[maxn];

void add_edge(int u,int v,int w){
	e[tot].to = v;
	e[tot].w = w;
	e[tot].next = head[u];
	head[u] = tot++;
}

for(int i=head[u];~i;i=e[i].next){
	int v = e[i].to;
	int w = e[i].w;
}

//init
memset(head , -1 , sizeof(head));

二分图判定

通过着色来判定，整个图只染两种颜色，如果相邻点颜色不同就是二分图

poj

dyh 发布于 2020-01-27 收录于 Poj

线段相交

1127

题意

判断两条线段是否相交，对于N条线段，间接相交也算相交。对于每次询问，判断给定的两条线段是否相交

题解

这个题目分成两部分，一部分是基础的判断两条线段是否相交，用一个bool数组来存储信息。另一部分是判断间接相交，可以用floyd-warshall（比较巧妙）或者并查集.第一部分就是套模板。

简易对拍

dyh 发布于 2020-01-27 收录于 Note

以这道题为例

准备一个对拍的文件夹，里面装这些东西

duipai_random_input_src.cpp是产生随机测试数据的代码

abc152-D

dyh 发布于 2020-01-26 收录于 Abc

题目链接题意：找正整数对（A,B），A、B都不大于N，满足A的第一个数字是B的最后一个数

字，B的第一个数字是A的最后一个数字，个位数也算，输出满足条件的正整数对的个数

排序算法的时间复杂度

dyh 发布于 2020-01-23 收录于 Note

时间复杂度与计算时间的关系

dyh 发布于 2020-01-23 收录于 Note

CP笔记

dyh 发布于 2020-01-19 收录于 Note

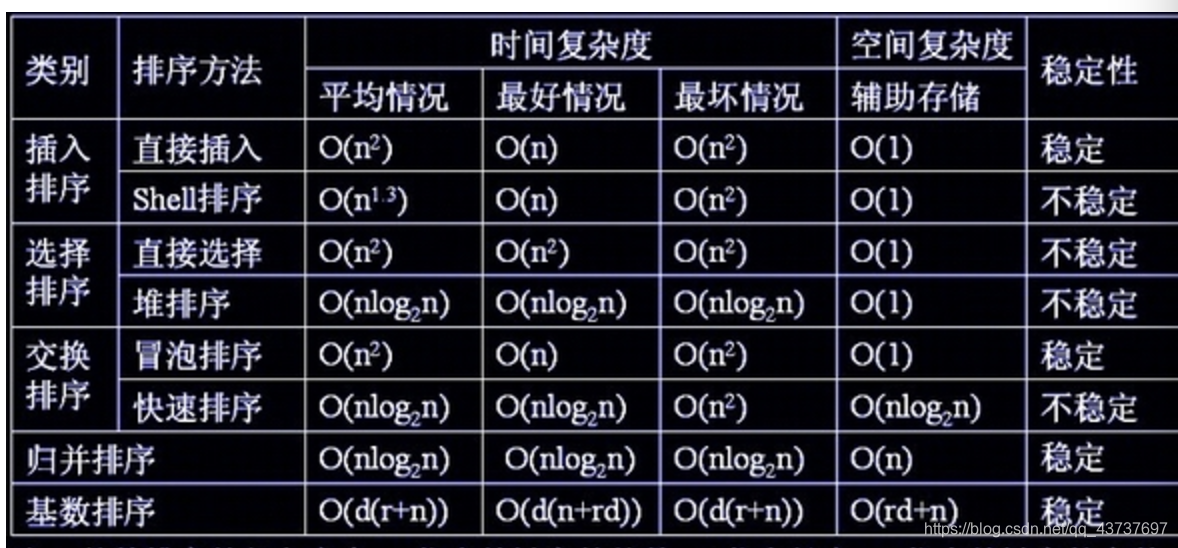
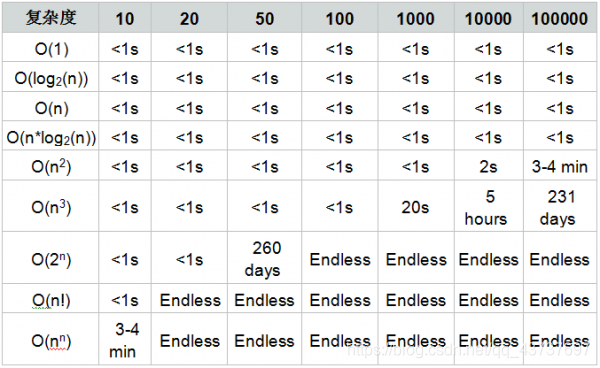
记录的东西十分零散，适用于速查，不适合系统学习

由于记录的时候所掌握的知识很浅，所以可能存在错误

快速排序

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


#include <bits/stdc++.h>

using namespace std;
using ll = long long;

void quicksort(int s[], int l, int r) {
    if (l < r) {
        int i = l, j = r, x = s[l];
        while (i < j) {
            while (i < j && s[j] >= x)
                j--;
            if (i < j)
                s[i++] = s[j];
            while (i < j && s[i] < x)
                i++;
            if (i < j)
                s[j--] = s[i];
        }
        s[i] = x;
        quicksort(s, l, i - 1);
        quicksort(s, i + 1, r);
    }
}

int main() {

    int a[10] = {3, 5, 1, 8, 9, 4, 2, 6, 0, 1};
    int i;
    quicksort(a, 1, 9);
    for (i = 0; i < 10; i++)
        cout << a[i] << ' ';
    

    return 0;
}

//3 0 1 1 2 4 5 6 8 9

产生随机数

古老的生成随机数的方法

c++交集、并集、差、对称差函数

dyh 发布于 2020-01-17 收录于 Note

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


#include<iostream>
#include<set>
//#include<map>
//#include<string>
#include<algorithm>
#include<iterator>
using namespace std;
int main()
{
	int a[]={3,2,1};
	int b[]={3,4,5,6};
	set<int> s1(a,a+3);
	set<int> s2(b,b+4);
	set<int> s3;
	set_union(s1.begin(),s1.end(),s2.begin(),s2.end(),inserter(s3,s3.begin()));
	for(set<int>::iterator it=s3.begin();it!=s3.end();it++)
		cout<<*it<<" ";
	cout<<endl;
	set_union(s1.begin(),s1.end(),s2.begin(),s2.end(),ostream_iterator<int>(cout,"*"));
	cout<<endl;
	set_intersection(s1.begin(),s1.end(),s2.begin(),s2.end(),ostream_iterator<int>(cout," "));
	cout<<endl;
	set_difference(s1.begin(),s1.end(),s2.begin(),s2.end(),ostream_iterator<int>(cout," "));
	cout<<endl;
	set_symmetric_difference(s1.begin(),s1.end(),s2.begin(),s2.end(),ostream_iterator<int>(cout," "));
	return 0;
}

c++每种类型的值域

dyh 发布于 2020-01-17 收录于 Note

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55


#include<iostream>
#include<string>
#include <limits>
using namespace std;
 
int main()
{
    cout << "type: \t\t" << "************size**************"<< endl;
    cout << "bool: \t\t" << "所占字节数：" << sizeof(bool);
    cout << "\t最大值：" << (numeric_limits<bool>::max)();
    cout << "\t\t最小值：" << (numeric_limits<bool>::min)() << endl;
    cout << "char: \t\t" << "所占字节数：" << sizeof(char);
    cout << "\t最大值：" << (numeric_limits<char>::max)();
    cout << "\t\t最小值：" << (numeric_limits<char>::min)() << endl;
    cout << "signed char: \t" << "所占字节数：" << sizeof(signed char);
    cout << "\t最大值：" << (numeric_limits<signed char>::max)();
    cout << "\t\t最小值：" << (numeric_limits<signed char>::min)() << endl;
    cout << "unsigned char: \t" << "所占字节数：" << sizeof(unsigned char);
    cout << "\t最大值：" << (numeric_limits<unsigned char>::max)();
    cout << "\t\t最小值：" << (numeric_limits<unsigned char>::min)() << endl;
    cout << "wchar_t: \t" << "所占字节数：" << sizeof(wchar_t);
    cout << "\t最大值：" << (numeric_limits<wchar_t>::max)();
    cout << "\t\t最小值：" << (numeric_limits<wchar_t>::min)() << endl;
    cout << "short: \t\t" << "所占字节数：" << sizeof(short);
    cout << "\t最大值：" << (numeric_limits<short>::max)();
    cout << "\t\t最小值：" << (numeric_limits<short>::min)() << endl;
    cout << "int: \t\t" << "所占字节数：" << sizeof(int);
    cout << "\t最大值：" << (numeric_limits<int>::max)();
    cout << "\t最小值：" << (numeric_limits<int>::min)() << endl;
    cout << "unsigned: \t" << "所占字节数：" << sizeof(unsigned);
    cout << "\t最大值：" << (numeric_limits<unsigned>::max)();
    cout << "\t最小值：" << (numeric_limits<unsigned>::min)() << endl;
    cout << "long: \t\t" << "所占字节数：" << sizeof(long);
    cout << "\t最大值：" << (numeric_limits<long>::max)();
    cout << "\t最小值：" << (numeric_limits<long>::min)() << endl;
    cout << "unsigned long: \t" << "所占字节数：" << sizeof(unsigned long);
    cout << "\t最大值：" << (numeric_limits<unsigned long>::max)();
    cout << "\t最小值：" << (numeric_limits<unsigned long>::min)() << endl;
    cout << "double: \t" << "所占字节数：" << sizeof(double);
    cout << "\t最大值：" << (numeric_limits<double>::max)();
    cout << "\t最小值：" << (numeric_limits<double>::min)() << endl;
    cout << "long double: \t" << "所占字节数：" << sizeof(long double);
    cout << "\t最大值：" << (numeric_limits<long double>::max)();
    cout << "\t最小值：" << (numeric_limits<long double>::min)() << endl;
    cout << "float: \t\t" << "所占字节数：" << sizeof(float);
    cout << "\t最大值：" << (numeric_limits<float>::max)();
    cout << "\t最小值：" << (numeric_limits<float>::min)() << endl;
    cout << "size_t: \t" << "所占字节数：" << sizeof(size_t);
    cout << "\t最大值：" << (numeric_limits<size_t>::max)();
    cout << "\t最小值：" << (numeric_limits<size_t>::min)() << endl;
    cout << "string: \t" << "所占字节数：" << sizeof(string) << endl;
    // << "\t最大值：" << (numeric_limits<string>::max)() << "\t最小值：" << (numeric_limits<string>::min)() << endl;
    cout << "type: \t\t" << "************size**************"<< endl;
    return 0;
}

extended euclidean algorithm

dyh 发布于 2020-01-17 收录于 Algorithm Note

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


#include<bits/stdc++.h>
using namespace std;
int ex_gcd(int a,int b,int& x,int& y)
{
	int t,res;
	if(!b)
	{
		x=1;y=0;return a;
	}
	else
	{
		res=ex_gcd(b,a%b,x,y);
		t=x;
		x=y;y=t-a/b*y;
		return res;
	}
}
int main()
{
	int a,b,x,y;
	a=60;
	b=22;
	cout<<ex_gcd(a,b,x,y)<<endl;
	cout<<x<<" "<<y<<endl;
	return 0;
}

ford fulkerson algorithm

dyh 发布于 2020-01-17 收录于 Algorithm Note

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79


//O(FE) 
/* 
input 
5 7
1 3 6
3 5 8
2 5 5
3 2 3
1 2 6
4 1 10
4 2 2
4 5
output
11
*/
#include<bits/stdc++.h>
using namespace std;
#define maxv 100
#define inf 0x3f3f3f3f
int v,e;
int s,t;
struct edge{int to,cap,rev;
};
vector<edge> G[maxv];
bool used[maxv];

void add_edge(int from ,int to,int cap)
{
	G[from].push_back((edge){to,cap,G[to].size()});
	G[to].push_back((edge){from,0,G[from].size()-1});
}

int dfs(int s,int t,int f)
{
	if(s==t) return f;
	used[s]=true;
	for(int i=0;i<G[s].size();i++)
	{
		edge &e =G[s][i];
		if(!used[e.to] && e.cap>0)
		{
			int d=dfs(e.to,t,min(f,e.cap));
			if(d>0)
			{
				e.cap-=d;
				G[e.to][e.rev].cap+=d;
				return d;
			}
		}
	}
	return 0;
}

int max_flow(int s,int t)
{
	int flow=0;
	for(;;)
	{
		memset(used,0,sizeof(used));
		int f=dfs(s,t,inf);
		if(f==0) return flow;
		flow+=f;
	}
}

int main()
{
	freopen("input.txt","r",stdin);
	cin>>v>>e;
	for(int i=0;i<e;i++)
	{
		int from,to,cap;
		scanf("%d%d%d",&from,&to,&cap);
		add_edge(from,to,cap);
	}
	cin>>s>>t;
	cout<<max_flow(s,t);
	return 0;
}