^_^

steep

dyh 发布于 2021-03-02 收录于 GAME

steep是育碧在2016年12月2日发行的滑雪游戏

在steam上要一百多，在育碧商城上免费

在很早以前就看过有人玩育碧的肖恩怀特滑雪

但是一直找不到，可能因为知名度很低

极限竞速地平线4

dyh 发布于 2021-03-02 收录于 GAME

Forza Horizon 4是微软在2018年10月2日发行的开车游戏

用xbox玩就很爽

风景做得很不错

有关汽车的专业知识做得很丰富

嘉年华的各种活动安排得很合理

整个游戏体系很完善

赛博朋克2077

dyh 发布于 2021-03-02 收录于 GAME

cyberpunk2077是CD Projekt RED开发的rpg游戏

经历了一次次跳票，终于在年底玩到这款游戏

小黑盒的评分

小黑盒社区的玩家评分并不高，很多人都很失望

非线性优化

dyh 发布于 2021-03-01 收录于 Note Slam

相机模型

dyh 发布于 2021-03-01 收录于 Note Slam

针孔相机模型

针孔相机模型和畸变模型把三维点投影到相机内的二维平面，构成相机的内参数（intrinsics）

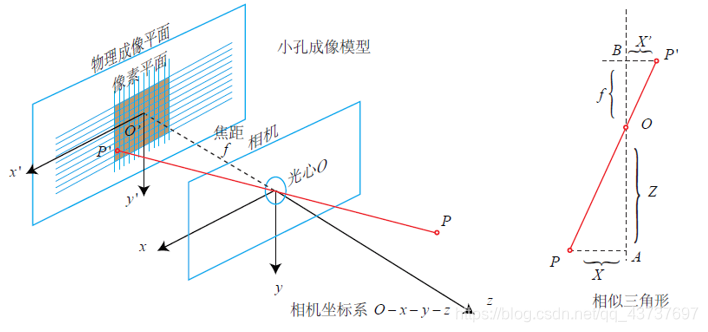
根据三角形的相似性

$$ \frac{Z}{f}=-\frac{X}{X^{\prime}}=-\frac{Y}{Y^{\prime}} $$

把成像平面翻转到前面

编译原理小练习

dyh 发布于 2021-01-21 收录于 Note Courses

随便记录一下

图源

词法分析程序设计

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81


import sys

#种别编码表
dict = {'begin' : 1, 'if' : 2, 'then' : 3, 'while' : 4, 'do' : 5, 'end' : 6,
        '+' : 13, '-' : 14, '*' : 15, '/' : 16, ':' : 17, ':=' : 18,
        '<' : 20, '<>' : 21, '<=' : 22, '>' : 23, '>=' : 24, '=' : 25, ';' : 26,
        '(' : 27, ')' : 28, '#' : 0}

#一些关键字
word = ['begin', 'if', 'then', 'while', 'do', 'end']


#s是关键字时的处理
def do_word(s):
    print('(%d, %s) ' % (dict[s], s), end='')

#s是id时的处理
def do_id(s):
    print('(%d, \'%s\') ' % (10, s), end='')

#s是数字时的处理
def do_num(s):
    print('(%d, %s) ' % (11, s), end='')

#s是符号时的处理
def do_symbol(s):
    print('(%d, %s) ' % (dict[s], s), end='')


def main():
    with open('in.txt', 'r') as f:
        tmpio = sys.stdin
        sys.stdin = f
        str = input()
        #print(str)
        i = 0
        while str[i] != '#':    # #是结束标志
            ch = str[i]
            if ch == ' ':       #空格直接跳过
                i += 1
                continue
            if ch.isalpha():    #如果是字母就一直搜素知道非数字和非字母，这样就能取到关键字或标识符
                tmp_str = ''
                while ch.isalnum():
                    tmp_str += ch
                    i += 1
                    ch = str[i]
                if tmp_str in word:     #如果是关键字
                    do_word(tmp_str)
                else :
                    do_id(tmp_str)      #否则是标识符
            elif ch.isnumeric():        #取得这个数字
                tmp_str = ''
                while ch.isnumeric():
                    tmp_str += ch
                    i += 1
                    ch = str[i]
                do_num(tmp_str)
            else:                       #判断是否是两个字符组成的符号
                tmp_str = ''
                if str[i] == ':' and str[i + 1] == '=':
                    tmp_str = ':='
                    i += 1
                elif str[i] == '<' and str[i + 1] == '>':
                    tmp_str = '<>'
                    i += 1
                elif str[i] == '<' and str[i + 1] == '=':
                    tmp_str = '<='
                    i += 1
                elif str[i] == '>' and str[i + 1] == '=':
                    tmp_str = '>='
                    i += 1
                else:
                    tmp_str = ch        #一个字符组成的符号
                do_symbol(tmp_str)
                i += 1
        print('(0, #)')
        sys.stdin = tmpio

if __name__ == '__main__':
    main()

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110


function func(){
    var tmp = document.getElementById('qwe');
    var str = tmp.value;

    var fstr = '';

    // tmp = document.getElementById('zxc');
    // tmp.value = str;

    function do_word(s) {
        fstr += '(';
        fstr += dict[s];
        fstr += ', ';
        fstr += s;
        fstr += ') ';
    }

    function do_id(s) {
        fstr += '(';
        fstr += 10;
        fstr += ', ';
        fstr += s;
        fstr += ') ';
    }

    function do_num(s) {
        fstr += '(';
        fstr += 11;
        fstr += ', ';
        fstr += s;
        fstr += ') ';
    }

    function do_symbol(s) {
        fstr += '(';
        fstr += dict[s];
        fstr += ', ';
        fstr += s;
        fstr += ') ';
    }


    function contains(arr, obj) {
        var i = arr.length;
        while (i--) {
            if (arr[i] === obj) {
                return true;
            }
        }
        return false;
    }


    var dict = {'begin' : 1, 'if' : 2, 'then' : 3, 'while' : 4, 'do' : 5, 'end' : 6,
        '+' : 13, '-' : 14, '*' : 15, '/' : 16, ':' : 17, ':=' : 18,
        '<' : 20, '<>' : 21, '<=' : 22, '>' : 23, '>=' : 24, '=' : 25, ';' : 26,
        '(' : 27, ')' : 28, '#' : 0};
    var word = new Array('begin', 'if', 'then', 'while', 'do', 'end');

    var i = 0;
    while(str[i] != '#'){
        var ch = str[i];
        if(ch == ' '){
            i++;
            continue;
        }
        if((ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z')){
            var tmp_str = '';
            while((ch >= 'a' && ch <= 'z') || (ch >= 'A' && ch <= 'Z') || (ch >= '0' && ch <= '9')){
                tmp_str += ch;
                i++;
                ch = str[i];
            }
            if(contains(word, tmp_str)){
                do_word(tmp_str);
            }else do_id(tmp_str);
        }else if(ch >= '0' && ch <= '9'){
            var tmp_str = '';
            while (ch >= '0' && ch <= '9'){
                tmp_str += ch;
                i++;
                ch = str[i];
            }
            do_num(tmp_str);
        }else{
            var tmp_str = '';
            if(str[i] == ':' && str[i + 1] == '='){
                tmp_str = ':=';
                i++;
            }else if(str[i] == '<' && str[i + 1] == '>'){
                tmp_str = '<>';
                i++;
            }else if(str[i] == '<' && str[i + 1] == '='){
                tmp_str = '<=';
                i++;
            }else if(str[i] == '>' && str[i + 1] == '='){
                tmp_str= '>=';
                i++;
            }else tmp_str = ch;
            do_symbol(tmp_str);
            i++;
        }
    }
    fstr += '(0, #)';


    tmp = document.getElementById('zxc');
    tmp.value = fstr;

}

基于语法制导翻译的表达式转换编译器

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232


function func2() {
        var tmp = document.getElementById('qwe');
        var str = tmp.value;

        var fstr = '';

        var st_lex = [];
        var st_tok = [];

        const NUM = 256, DIV = 257, MOD = 258, ID = 259, DONE = 260, NONE = -1, EOSTR = '\0';

        const BUF_SIZE = 100, SYM_SIZE = 200;

        var lookahead, lineno = 1, tokenval = NONE;

        var lexbuf = '';

        var I = 0;

        var eflag = false;

        var estr = '';

        function emit(type, tval) {
            switch (type) {
                case '+':
                case '-':
                case '*':
                case '/':
                    fstr += type;
                    break;
                case DIV:
                    fstr += 'div';
                    break;
                case MOD:
                    fstr += 'mod';
                    break;
                case NUM:
                    fstr += tval;
                    break;
                case ID:
                    fstr += st_lex[tval];
                    break;
                default:
                    return;
            }
        }

        function error(s) {
            fstr += 'line ' + lineno + ': ' + s + '\n';
            eflag = true;
            estr = fstr;
            //add a teiminate statement
            tmp = document.getElementById('zxc');
            tmp.value = fstr;
            //alert('qqq');
            throw new  Error ('error');
        }

        function insert(s, num) {
            if(st_lex.length >= SYM_SIZE){
                error('symbol table full');
            }
            st_lex.push(s);
            st_tok.push(num);
        }

        function init() {
            insert('', 0);
            insert('div', DIV);
            insert('mod', MOD);
        }

        function lookup(s) {
            for(var i = 1; i < st_lex.length; ++i){
                if(st_lex[i] == s) return i;
            }
            return 0;
        }

        function lex() {
            var tmp;
            while(true){
                tmp = str[I];
                I++;
                if(tmp == ' ' || tmp == '\t') continue;
                else if(tmp == '\n'){
                    lineno++;
                }else if(tmp >= '0' && tmp <= '9'){
                    I--;
                    var tt = '';
                    while(tmp >= '0' && tmp <= '9'){
                        tt += tmp;
                        I++;
                        tmp = str[I];
                    }
                    tokenval = parseInt(tt);
                    return NUM;
                }else if((tmp >= 'a' && tmp <= 'z') || (tmp >= 'A' && tmp <= 'Z')){
                    var pos, ind = 0;
                    lexbuf = '';
                    while ((tmp >= 'a' && tmp <= 'z') || (tmp >= 'A' && tmp <= 'Z') || (tmp >= '0' && tmp <= '9')){
                        lexbuf += tmp;
                        tmp = str[I];
                        I++;
                        ind++;

                        var tmps = lexbuf;
                        if(tmps == 'DIV' || tmps == 'MOD'){
                            break;
                        }
                        if(ind >= BUF_SIZE){
                            error('the length of identifier is too long');
                        }
                    }

                    if(tmp != '#'){
                        I--;
                    }


                    pos = lookup(lexbuf);
                    if(pos == 0){
                        insert(lexbuf, ID);
                        tokenval = st_lex.length - 1;
                        return ID;
                    }else if(st_lex[pos] == 'div' || st_lex[pos] == 'mod'){
                        if(st_lex[pos] == 'div'){
                            tokenval = DIV;
                            return DIV;
                        }else {
                            tokenval = MOD;
                            return MOD;
                        }
                    }else {
                        tokenval = pos;
                        return ID;
                    }

                }else if(tmp == '#'){
                    return DONE;
                }else{
                    tokenval = NONE;
                    return tmp;
                }
            }
        }

        function match(x) {
            if(lookahead == x){
                lookahead = lex();
            }else error('syntax error');
        }

        function factor() {
            switch (lookahead) {
                case '(':
                    match('(');
                    express();
                    match(')');
                    break;
                case NUM:
                    emit(NUM, tokenval);
                    match(NUM);
                    break;
                case ID:
                    emit(ID, tokenval);
                    match(ID);
                    break;
                default:
                    error('syntax error');
            }
        }


        function term() {
            var tmp;
            factor();
            while(true){
                switch (lookahead) {
                    case '*':
                    case '/':
                    case DIV:
                    case MOD:
                        tmp = lookahead;
                        match(lookahead);
                        factor();
                        emit(tmp, NONE);
                        continue;
                    default:
                        return ;
                }
            }
        }


        function express() {
            var tmp;
            term();
            while (true){
                switch (lookahead) {
                    case '+':
                    case '-':
                        tmp = lookahead;
                        match(lookahead);
                        term();
                        emit(tmp, NONE);
                        continue;
                    default:
                        return ;
                }
            }
        }

        function parse() {
            lookahead = lex();
            while (lookahead != DONE){
                express();
                match(';');
                fstr += '\n';
            }
        }

        init();
        parse();

        tmp = document.getElementById('zxc');
        tmp.value = fstr;
        //if(eflag) tmp.value = estr; else tmp.value = fstr;


    }

说明语句的词法分析器

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124


import sys



ind = 0
id = []     #存标识符名称
tp = []     #存标识符类型
val = []    #存标识符的值



def judge_is_id(s):     #是否满足标识符的条件
    if s.count(' ') > 0:
        return False
    if not s[0].isalpha():
        return False
    return True

def main():
    with open('in.txt', 'r') as f:
        tmpio = sys.stdin
        sys.stdin = f
        str = input()

        int_num = char_num = string_num = float_num = 0     #计数

        i = 0
        while str[i] != ';':        #分号表示结束
            if str[i] == ' ':       #空格跳过
                i += 1
                continue

            if str[i] != 'c':       #第一个字符不为c，说明不是const
                print('It is not a constant declaration statement!')
                print('Please input a string again!')
                sys.exit()
            elif i + 6 > len(str):  #说明不存在const这个单词
                print('It is not a constant declaration statement!')
                print('Please input a string again!')
                sys.exit()
            elif str[i : i + 5] != 'const':     #开头是c但是单词不是const
                print('It is not a constant declaration statement!')
                print('Please input a string again!')
                sys.exit()
            else:
                str = str[i + 5: -1]        #是const，截掉这个单词
                break

        i = 0
        foo = str.split(',')            #按逗号分割
        #print(foo)

        for cnt in foo:
            left = (cnt.split('=')[0])      #等号左边的量
            right = cnt.split('=')[1]       #等号右边的数值
            left = left.strip()             #消掉前后的空格
            right = right.strip()

            if not judge_is_id(left):       #不是标识符
                id.append(left)
                tp.append('Wrong! It is not an identifier!')
                val.append(' ')
                #print('Wrong! It is not an identifier!')
                #sys.exit()
            else:
                left.strip()
                id.append(left)



                if right[0] == '\'' and right[2] == '\'' :      #值所代表的的字符串中有两个单引号，且距离为1，说明是char类型
                    tp.append('char')
                    val.append(right[1])
                elif right.count('\'') == 2:                #有两个单引号，但是其中的字符大于1
                    tp.append('more than one character in \'')
                    val.append(' ')
                    #print('more than one character in \'\'')
                    #sys.exit()
                elif right.count('\"') == 2:            #有两个双引号是string类型
                    tp.append('string')
                    val.append(right[1: -1])
                else :                                  #剩下的情况是数字或非法
                    if right.count('.') == 1 and right.split('.')[0].isdigit() and right.split('.')[1].isdigit() :
                        if right.split('.')[0][0] == '0':       #上面的语句说明含有一个小数点，且小数点左右两边都是数字，这可能是个小数
                            tp.append('numbers cannot started with zero')   #有前导0不行，这里没有考虑0.xxx的情况
                            val.append(' ')
                            #print('numbers cannot started with zero')
                            #sys.exit()
                        else:                   #合法的小数
                            tp.append('float')
                            val.append(right)

                    elif not right.isdigit():       #含有非数字成分，说明这不是一个数字
                        tp.append('Wrong constant')
                        val.append(' ')
                        #print('Wrong constant')
                        #sys.exit()
                    elif right[0] == '0':       #是数字但是含有前导0
                        tp.append('numbers cannot started with zero')
                        val.append(' ')
                        #print('numbers cannot started with zero')
                        #sys.exit()
                    else :                      #合法的数字
                        tp.append('integer')
                        val.append(right)


        #print(len(id), len(tp), len(val))
        bar = len(id)                           #输出
        for i in range(bar):
            print('%s ( %s, %s )' % (id[i], tp[i], val[i]))

        for i in range(bar):                    #统计
            if tp[i] == 'integer':  int_num += 1
            if tp[i] == 'char': char_num += 1
            if tp[i] == 'string':   string_num += 1
            if tp[i] == 'float':    float_num += 1

        print('%s = %d, %s =  %d, %s = %d, %s = %d' % ('int_num', int_num, 'char_num', char_num, 'string_num', string_num, 'float_num', float_num) )

        sys.stdin = tmpio

if __name__ == '__main__':
    main()

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118


function func3() {

    var tmp = document.getElementById('qwe');
    var str = tmp.value;
    var fstr = '';

    var id = [], tp = [], val = [];

    function judge_is_id(s) {
        if ((s.split(' ')).length - 1 > 0){
            return false;
        }
        if(!((s[0] >= 'a' && s[0] <= 'z') || (s[0] >= 'A' || s[0] <= 'Z'))){
            return false;
        }
        return true;
    }

    var int_num, char_num, string_num, float_num;
    int_num = char_num = string_num = float_num = 0;

    var i = 0;
    while (str[i] != ';'){
        if(str[i] == ' '){
            i++;
            continue;
        }
        if(str[i] != 'c'){
            fstr += 'It is not a constant declaration statement!\n';
            fstr += 'Please input a string again!';
            tmp = document.getElementById('zxc');
            tmp.value = fstr;
            throw new Error('error');
        }else if(i + 6 > str.length){
            fstr += 'It is not a constant declaration statement!\n';
            fstr += 'Please input a string again!';
            tmp = document.getElementById('zxc');
            tmp.value = fstr;
            throw new Error('error');
        }else if(str.slice(i, i + 5) != 'const'){
            fstr += 'It is not a constant declaration statement!\n';
            fstr += 'Please input a string again!';
            tmp = document.getElementById('zxc');
            tmp.value = fstr;
            throw new Error('error');
        }else{
            str = str.slice(i + 5, str.length - 1);
            break;
        }
    }

    var foo = str.split(',');

    for(i = 0; i < foo.length; ++i){
        var cnt = foo[i];
        var left = cnt.split('=')[0];
        var right = cnt.split('=')[1];

        left = left.replace(/(^\s*)|(\s*$)/g, "");
        right = right.replace(/(^\s*)|(\s*$)/g, "");

        if(!judge_is_id(left)){
            id.push(left);
            tp.push('Wrong! It is not an identifier!');
            val.push(' ');
        }else {
            id.push(left);

            if(right[0] == '\'' && right[2] == '\''){
                tp.push('char');
                val.push(right[1]);
            }else if((right.split('\'')).length - 1 == 2){
                tp.push('more than one character in \'');
                val.push(' ');
            }else if((right.split('\"')).length - 1 == 2){
                tp.push('string');
                val.push(right.slice(1, right.length - 1));
            }else{
                if((right.split('.')).length - 1 == 1 && !isNaN(right.split('.')[0]) && !isNaN(right.split('.')[1])){
                    if(right.split('.')[0][0] == '0'){
                        tp.push('numbers cannot started with zero');
                        val.push(' ');
                    }else{
                        tp.push('float');
                        val.push(right);
                    }
                }else if(isNaN(right)){
                    tp.push('Wrong constant');
                    val.push(' ');
                }else if(right[0] == '0'){
                    tp.push('numbers cannot started with zero');
                    val.push(' ');
                }else{
                    tp.push('integer');
                    val.push(right);
                }
            }

        }

    }

    var bar = id.length;
    for(i = 0; i < bar; ++i){
        fstr += (id[i] + ' ( ' + tp[i] + ' , ' + val[i] + ' ) \n');
    }
    for(i = 0; i < bar; ++i){
        if(tp[i] == 'integer') int_num++;
        if(tp[i] == 'char') char_num++;
        if(tp[i] == 'string') string_num++;
        if(tp[i] == 'float') float_num++;
    }
    fstr += ('int_num = ' + int_num + ', char_num = ' + char_num + ', string_num = ' + string_num + ', float_num = ' + float_num);
    tmp = document.getElementById('zxc');
    tmp.value = fstr;


}

基于预测分析方法的表达式语法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87


import sys

#预测分析表

dict = {
    'S' : {
        'm' : 'AT',
        '(' : 'AT'
    },
    'T' : {
        '+' : '+AT',
        ')' : '$',
        '#' : '$',
    },
    'A' : {
        'm' : 'BU',
        '(' : 'BU'
    },
    'U' : {
        '+' : '$',
        '*' : '*BU',
        ')' : '$',
        '#' : '$'
    },
    'B' : {
        'm' : 'm',
        '(' : '(S)'
    }
}

#非终结符

no_tm = ['m', '+', '*', '(', ')', '#']

#输出一行包含序号，分析栈，输入栈，所用产生式

def PRINT(no, stk, s, pd):
    if stk[-1:] not in no_tm:
        print('%d\t%-10s%10s\t%s->%s' % (no, stk, s, stk[-1:], pd))
    else :
        print('%d\t%-10s%10s\t%s' % (no, stk, s, pd))


def main():
    with open('in.txt', 'r') as f:
        tmpio = sys.stdin
        sys.stdin = f
        stri = input()

        num = 1         #序号
        prod = ''       #产生式
        ind = 0         #输入串的下标
        stack = '#S'    #分析栈


        while len(stack) != 1:          #说明只剩#
            if stack[-1:] == stri[ind]:     #分析栈的栈顶等于输入串的栈顶，说明非终结符匹配
                PRINT(num, stack, stri, '\'' + stri[ind] + '\' match')
                stri = ' ' * (ind + 1) + stri[ind+1:]
                ind += 1
                num += 1
                stack = stack[:-1]
            elif stack[-1:] in no_tm:       #分析栈的栈顶不等于输入串的栈顶又不是非终结符，说明不匹配
                PRINT(num, stack, stri, '[ERROR] not match')
                sys.exit()
            elif stri[ind] not in dict[stack[-1:]].keys():      #在预测分析表中没有填产生式，出错
                PRINT(num, stack, stri, '[ERROR] not match')
                sys.exit()
            else:                                       #利用产生式，出栈和入栈
                prod = dict[stack[-1:]][stri[ind]]
                PRINT(num, stack, stri, prod)
                num += 1
                stack = stack[:-1]
                if prod != '$':
                    stack += prod[::-1]

        PRINT(num, stack, stri, 'acc')                  #出错的全都中途退出了，能走到这步的都是acc






        sys.stdin = tmpio

if __name__ == '__main__':
    main()

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101


function func4() {

    var tmp = document.getElementById('qwe');
    var str = tmp.value;
    var fstr = '';

    var dict = {
        'S' : {
            'm' : 'AT',
            '(' : 'AT'
        },
        'T' : {
            '+' : '+AT',
            ')' : '$',
            '#' : '$',
        },
        'A' : {
            'm' : 'BU',
            '(' : 'BU'
        },
        'U' : {
            '+' : '$',
            '*' : '*BU',
            ')' : '$',
            '#' : '$'
        },
        'B' : {
            'm' : 'm',
            '(' : '(S)'
        }
    };

    no_tm = ['m', '+', '*', '(', ')', '#'];

    function PRINT(no, stk, s, pd) {
        var tchar = stk.slice(stk.length - 1, stk.length);
        if(no_tm.indexOf(tchar) == -1){
            while(stk.length < 20){
                stk += ' ';
            }
            while (s.length < 20){
                s = ' ' + s;
            }
            fstr += no;
            fstr += ('\t' + stk + s + '\t\t\t' + tchar + '->' + pd + '\n');
        }else{
            while(stk.length < 20){
                stk += ' ';
            }
            while (s.length < 20){
                s = ' ' + s;
            }
            fstr += no;
            fstr += ('\t' + stk + s + '\t\t\t' + pd + '\n');
        }
    }


    var num = 1;
    var ind = 0;
    var stack = '#S';

    while (stack.length != 1){
        if(stack.slice(stack.length - 1, stack.length) == str[ind]){
            PRINT(num, stack, str, '\'' + str[ind] + '\' match');
            tt_str = str;
            str = '';
            for(var j = 0; j < ind + 1; ++j){
                str += ' ';
            }
            str += tt_str.slice(ind + 1, tt_str.length);
            ind++;
            num++;
            stack = stack.slice(0, stack.length - 1);
        }else if(no_tm.indexOf(stack.slice(stack.length - 1, stack.length)) != -1){
            PRINT(num, stack, str, '[ERROR] not match');
            tmp = document.getElementById('zxc');
            tmp.value = fstr;
            throw new Error('error');
        }else if(!(str[ind] in dict[stack.slice(stack.length - 1, stack.length)])){
            PRINT(num, stack, str, '[ERROR] not match');
            tmp = document.getElementById('zxc');
            tmp.value = fstr;
            throw new Error('error');
        }else{
            var prod = dict[stack.slice(stack.length - 1, stack.length)][str[ind]];
            PRINT(num, stack, str, prod);
            num++;
            stack = stack.slice(0, stack.length - 1);
            if(prod != '$'){
                stack += prod.split("").reverse().join("");
            }
        }
    }

    PRINT(num, stack, str, 'acc');

    tmp = document.getElementById('zxc');
    tmp.value = fstr;

}

9th hhucpc (Senior)

dyh 发布于 2020-12-09 收录于 Problemlist

u1s1,zyyyyy出的题目真的好好，补题的过程学到了好多（好菜啊o(╥﹏╥)o

题目链接

只贴了代码，题解参考此处

Codeforces Round #688 (Div. 2) A~D

dyh 发布于 2020-12-05 收录于 Codeforces

A. Cancel the Trains

题意

给一个铁路网，和每个火车所在的铁路（都在起点），每一时刻走一格，问有几辆车会相撞

题解

编号相同的横向和列向火车会相撞

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


#include "bits/stdc++.h"
using namespace std;
using ll = long long;
int a[105];
int b[105];
int main() {
    int _;
    cin >> _;
    while (_--) {
        int n, m;
        cin >> n >> m;
        for(int i = 0; i < n; ++i){
           cin >> a[i];
        }
        for(int i = 0; i < m; ++i){
            cin >> b[i];
        }
        int num = 0;
        for(int i = 0; i < n; ++i){
            for(int j = 0; j < m; ++j){
                if(a[i] == b[j]) num++;
            }
        }
        cout << num << endl;
    }
    return 0;
}

B. Suffix Operations

题意

给一个数组，刚开始时可以选择将一个数改成任何数，也可以不改，做以下操作直到每个数相等

abc184

dyh 发布于 2020-12-02 收录于 Abc

A - Determinant

题意

求二阶行列式

题解

1
2
3
4
5
6
7
8
9


#include "bits/stdc++.h"
using namespace std;
using ll = long long;
int main() {
    int a, b, c, d;
    cin >> a >> b >> c >> d;
    cout << a * d - c * b << endl;
    return 0;
}

B - Quizzes

题意

给n个问题，和答题情况，答对加1，答错减1（为0不扣分），初始分数x，求最终分数

8086指令系统

dyh 发布于 2020-11-07 收录于 Note Courses

8086寄存器

mem 存储器操作数

acc 累加器操作数

dest 目标操作数

src 源操作数

disp 8位或16位偏移量，可用符号地址表示

DATA 8位或16位数据

port 输入输出端口

李群与李代数

dyh 发布于 2020-11-07 收录于 Note Slam

群

与视觉slam有关的群

三维旋转矩阵构成了特殊正交群(special orthogonal group)

$$S O(3)=\left\{R \in \mathbb{R}^{3 \times 3} \mid R R^{T}=I, \operatorname{det}(R)=1\right\}$$

三维变换矩阵构成了特殊欧氏群（special euclidean group）

$$SE(3)=\left\{T=\left[\begin{array}{cc}R & t \\0^{T} & 1\end{array}\right] \in \mathbb{R}^{4 \times 4} \mid R \in SO(3), t \in \mathbb{R}^{3}\right\} $$

三维空间的刚体运动

dyh 发布于 2020-10-23 收录于 Note Slam

内积与外积

内积

外积

定义 ^ 符号

欧氏变换

euclidean transform

单次欧氏变换

同一个向量在两个坐标系中的表示，坐标系的变换包括一次旋转和一次平移

^_^

steep

极限竞速地平线4

赛博朋克2077

非线性优化

相关知识

矩阵求导

全概率公式

相机模型

针孔相机模型

编译原理小练习

词法分析程序设计

基于语法制导翻译的表达式转换编译器

说明语句的词法分析器

基于预测分析方法的表达式语法

9th hhucpc (Senior)

Codeforces Round #688 (Div. 2) A~D

A. Cancel the Trains

题意

题解

B. Suffix Operations

题意

abc184

A - Determinant

题意

题解

B - Quizzes

题意

8086指令系统

李群与李代数

群

三维空间的刚体运动

内积与外积

欧氏变换

单次欧氏变换