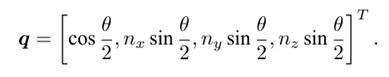三维空间的刚体运动
内积与外积
内积
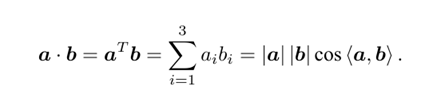
外积
定义 ^ 符号
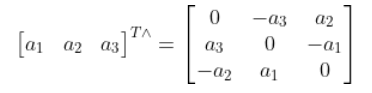
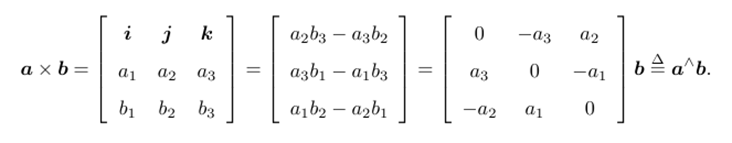
欧氏变换
euclidean transform
单次欧氏变换
同一个向量在两个坐标系中的表示,坐标系的变换包括一次旋转和一次平移

旋转


R为旋转矩阵(rotation matrix),它是一个行列式为1的正交矩阵(又叫特殊正交矩阵)(正交矩阵即逆为自身转置的矩阵)。反之,行列式为1的正交矩阵也是一个旋转矩阵,所以可以将n维旋转矩阵的集合定义为
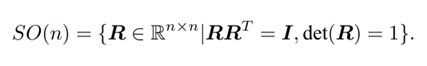
SO(n) 是特殊正交群 (special orthogonal group)
$$ a{}’=R^{-1}a=R^Ta $$
R的逆矩阵或转置矩阵刻画了相反的旋转
平移
$$ a{}’=Ra+t $$
$$ a_1=R_{12}a_2+t_{12} $$
t12表示2到1的变换
注意 t12 != -t21
多次欧氏变换

由于这种形式在多次变换之后会显得很冗长,所以采取以下措施
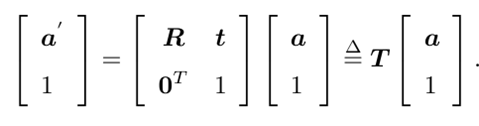
其中T是变换矩阵(transform matrix),a转变成齐次坐标
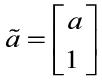
这样多次转换就变成

(约定之后的Ta,a就是齐次坐标化的,而Ra,a就是原来的)
对于变换矩阵T,满足该形式的矩阵可以构成特殊欧氏群(special euclidean group)

T的逆表示相反的变换
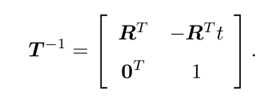
旋转向量
由于旋转矩阵用16个量来表达6个自由度的变换显得很多余,为了减少变量,引入旋转向量
实际上,任意的旋转都可以有旋转轴和旋转角度来刻画
假设旋转轴为一个单位长度的向量n,旋转角度为θ
根据罗德里格斯公式(rodrigues’s formula)
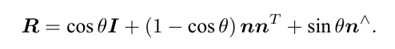
对等式两边求迹(trace)得到角度的表示

由于旋转轴上的向量在旋转后不发生变化,所以
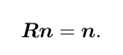
n是R在特征值为1时的特征向量
欧拉角
由于旋转向量和旋转矩阵不够直观,所以引入欧拉角
欧拉角把旋转分解成绕三个轴各自的旋转,由于分解方式很多,这里介绍最著名的rpy角
yaw-pitch-roll
绕物体的z轴旋转,得到yaw
绕旋转之后的y轴旋转,得到pitch
绕旋转之后的x轴旋转,得到roll

欧拉角的重大缺点就是万向锁问题(gimbal lock),当某个轴旋转90度时,第一次旋转和第三次旋转将使用同一个轴,这样就散失了一个自由度(这被称为奇异性问题),理论上可以证明,只要想用3个实数来表达三维旋转,都会出现奇异性问题,所以很少在slam中使用欧拉角,只用来验证自己的算法
四元数
复数
欧拉公式
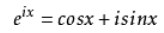
把复平面的向量旋转x度,相当于乘上e^(ix)
四元数的定义
它有1个实部,3个虚部,虚部分别对应空间坐标系的三个坐标轴

自己和自己的运算像复数,自己和别人的运算像叉乘
乘以i相当于绕轴旋转180度,i^2=-1意味着绕i轴旋转360度后得到一个相反的东西(这是个定义)
补充 ijk = -1
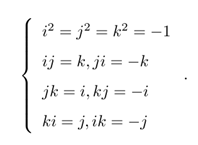
四元数也可以这样表示
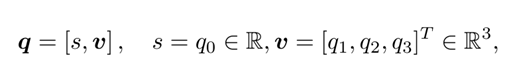
四元数的运算
加减法

乘法

向量形式
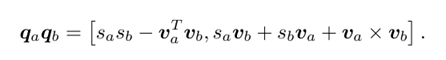
模长

共轭

四元数共轭与其本身相乘会得到一个实四元数,其实部为模长的平方
$$ q^*q=qq*=[s_a ^ 2 + v^Tv, 0]^T $$
逆
如果q为单位四元数,其逆和共轭就是同一个量
$$ qq^{-1}=q^{-1}q=1 $$
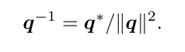
乘法的逆类似于矩阵
$$ (q_aq_b)^{-1} = q_b^{-1}q_a^{-1} $$
数乘
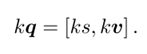
点乘
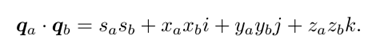
四元数表示旋转
假设点p = [x, y, z] 是最初的点,旋转后变成 p'
先将p变成虚四元数
$$ p = [0, x, y, z]^T = [0, v]^T $$
p’可以这样求得
$$ p{}’=qpq^{-1} $$
这里的乘法均为四元数乘法,结果也是四元数。最后把p’的虚部取出,就是旋转后的坐标。可以验证,计算后的实部为0
四元数到其他旋转表示的变换
假设
$$ q=[s,v]^T $$ $$ q=[q_0, q_1,q_2, q_3]^T $$
从四元数得到旋转矩阵
$$ R=vv^T + s^2I+2sv^{\wedge}+(v^{\wedge})^2 $$
从四元数得到旋转向量
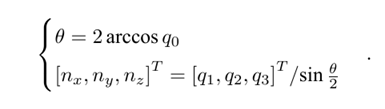
从旋转向量到四元数