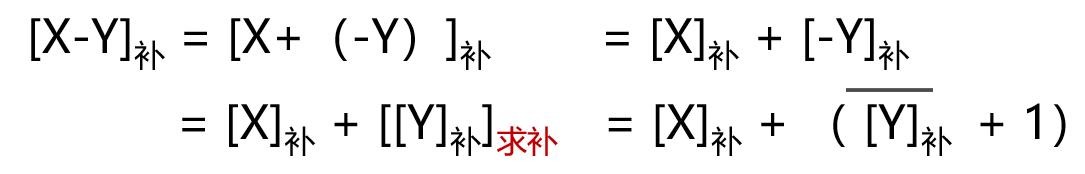二进制编码

二进制转十进制

除2取余

十进制转二进制

乘2次幂

小数进制转换

e.g.

3.59375

整数部分3的二进制位11

小数部分0.59375

0.59375*2=1.1875 ———————— 1

0.1875*2=0.375 —————————0

0.375*2=0.75 ——————————0

0.75*2=1.5 ——————————–1

0.5*2=1 ———————————–1

二进制位0.10011

所以3.59375的二进制表示为11.10011

有些小数不能测出现循环

IEEE754标准的浮点数与十进制数的转换

32位和64位标准

通过全1和全0来划定它的表示范围

E.G.

原码

即正常的二进制码（带符号位）

补码

正数（包括+0）的补码和原码一样

负数（包括-0）的补码在原码的基础上“按位取反，末尾加1”

补码转原码的一种方法

还可以用逆过程法，即减1取反

反码

正数（包括+0）的补码和原码一样

负数（包括-0）的补码在原码的基础上“按位取反”

补码的加法运算

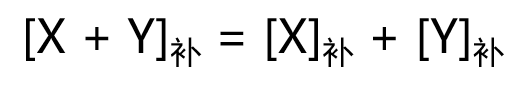
补码的减法运算