相机模型

针孔相机模型

针孔相机模型和畸变模型把三维点投影到相机内的二维平面，构成相机的内参数（intrinsics）

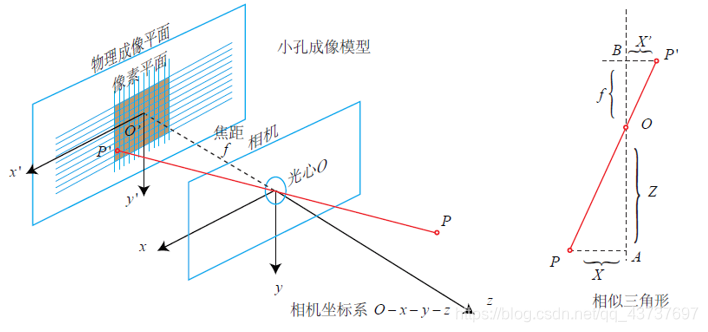
根据三角形的相似性

$$ \frac{Z}{f}=-\frac{X}{X^{\prime}}=-\frac{Y}{Y^{\prime}} $$

把成像平面翻转到前面

$$ \frac{Z}{f}=\frac{X}{X^{\prime}}=\frac{Y}{Y^{\prime}} $$

$$ \begin{array}{l}X^{\prime}=f \frac{X}{Z} \\ Y^{\prime}=f \frac{Y}{Z}\end{array} $$

把成像平面投影到像素平面

像素坐标系和成像坐标系之间相差了一个缩放和原点的平移

用u轴和v轴表示像素坐标系

设像素坐标系在u轴上缩放了α倍，在v轴上缩放了β倍，原点平移了[cx, cy]T，投影坐标和像素坐标的关系是

$$ \left\{\begin{array}{l}u=\alpha X^{\prime}+c_{x} \\ v=\beta Y^{\prime}+c_{y}\end{array}\right. $$

代入此式

$$ \begin{array}{l}X^{\prime}=f \frac{X}{Z} \\Y^{\prime}=f \frac{Y}{Z}\end{array} $$

fx=αf，fy=βf

$$ \left\{\begin{array}{l}u=f_{x} \frac{X}{Z}+c_{x} \\v=f_{y} \frac{Y}{Z}+c_{y}\end{array}\right. $$

将上式矩阵化（左侧是齐次式，右侧是非齐次式）

$$ \left(\begin{array}{l}u \\v \\1\end{array}\right)=\frac{1}{Z}\left(\begin{array}{ccc}f_{x} & 0 & c_{x} \\0 & f_{y} & c_{y} \\0 & 0 & 1\end{array}\right)\left(\begin{array}{l}X \\Y \\Z\end{array}\right) \triangleq \frac{1}{Z} K P $$

一般习惯这样写

$$ Z\left(\begin{array}{l}u \\v \\1\end{array}\right)=\left(\begin{array}{ccc}f_{x} & 0 & c_{x} \\0 & f_{y} & c_{y} \\0 & 0 & 1\end{array}\right)\left(\begin{array}{l}X \\Y \\Z\end{array}\right) \triangleq K P $$

K就是相机的内参数（camera intrinsics），在相机出厂时已经固定，是个常量

有些相机生产厂商会告诉你内参，有些不会。需要自己确定相机内参就叫做标定

在最开始的问题中，拿一个坐标点p进行投影。但这个p是相对于相机的坐标，实际应该是相对于世界的坐标Pw，所以要做一个转换。这个转换实际上只需要做一个旋转和平移就行，这在之前已经讨论过

假设相机的位姿由旋转矩阵R和平移向量t表示，那么世界坐标系到相机坐标系的转换如下

$$ Z P_{u v}=Z\left[\begin{array}{l}u \\v \\1\end{array}\right]=K\left(R P_{w}+t\right)=K T P_{w} $$

T为变换矩阵，=KTPw这个式子隐含了一次齐次坐标到非齐次坐标的转换

相机的位姿R，t为相机的外参（camera extrinsics）

归一化处理，令z=1，即所有的点都假设在归一化平面上

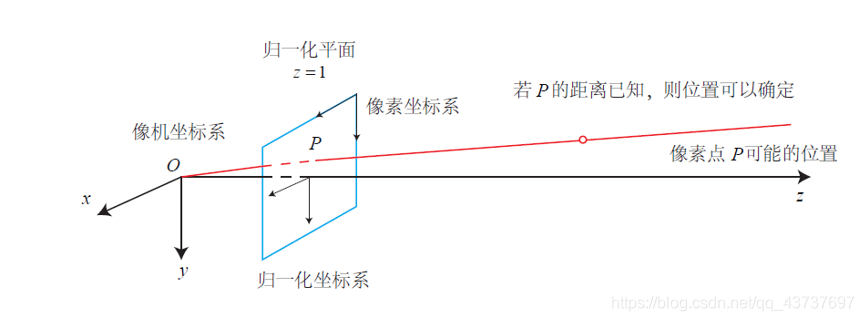
$$ \left(R P_{\mathrm{w}}+t\right)=\underbrace{[X, Y, Z]^{\mathrm{T}}}_{\text {相机坐标 }} \rightarrow \underbrace{[X / Z, Y / Z, 1]^{\mathrm{T}}}_{\text {归一化坐标 }} . $$

这样归一化坐标左乘内参就可以得到像素坐标，上式也说明单目视觉中点的深度信息丢失了

投影的顺序：世界-相机-归一化平面-像素

畸变模型

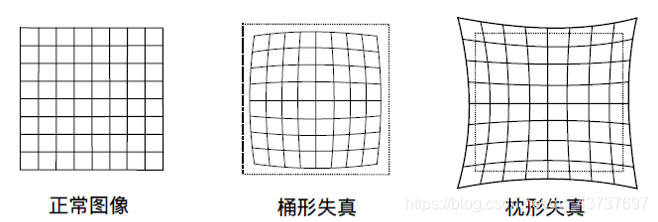
畸变（distortion）又叫失真，类似于这样

径向畸变由透镜形状引起的，分为桶形畸变和枕形畸变。

桶形畸变：放大率随着与光轴之间距离增加而减小

枕形畸变：放大率随着与光轴之间距离增加而增加

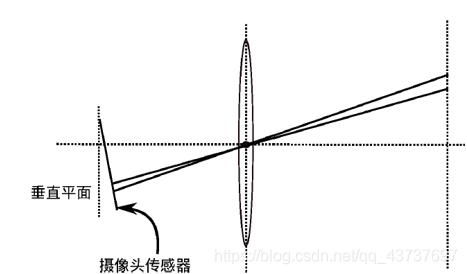
切向畸变是成像平面与透镜不平行引起的

数学表示径向畸变和切向畸变

考虑归一化平面（z=1）上的一点p，坐标[x,y]T，极坐标[r,θ]T

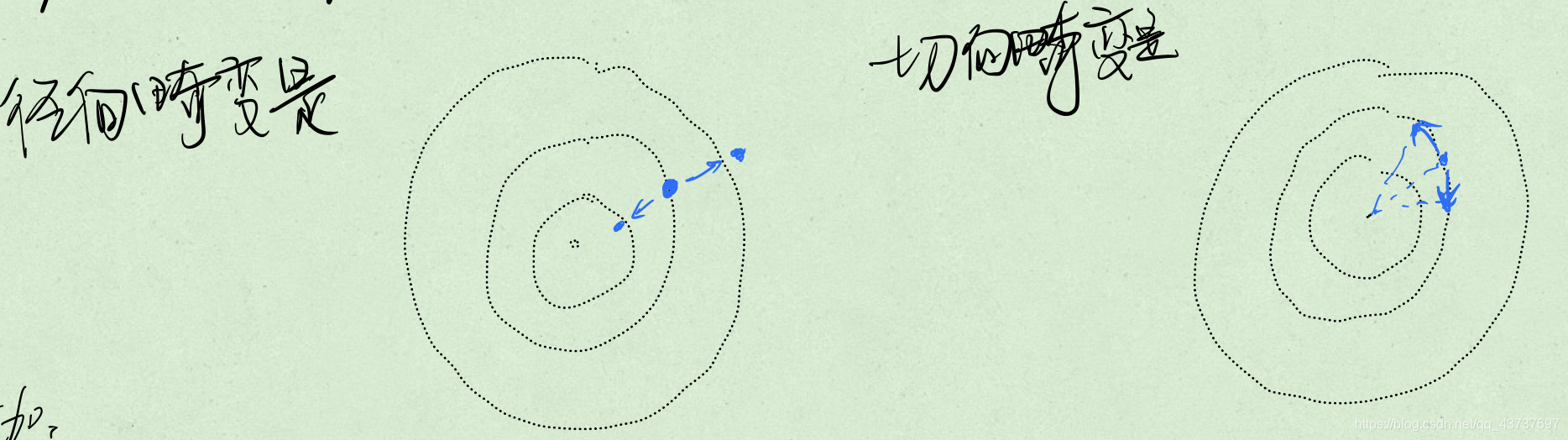
附加：如何理解切向畸变就是发生旋转？

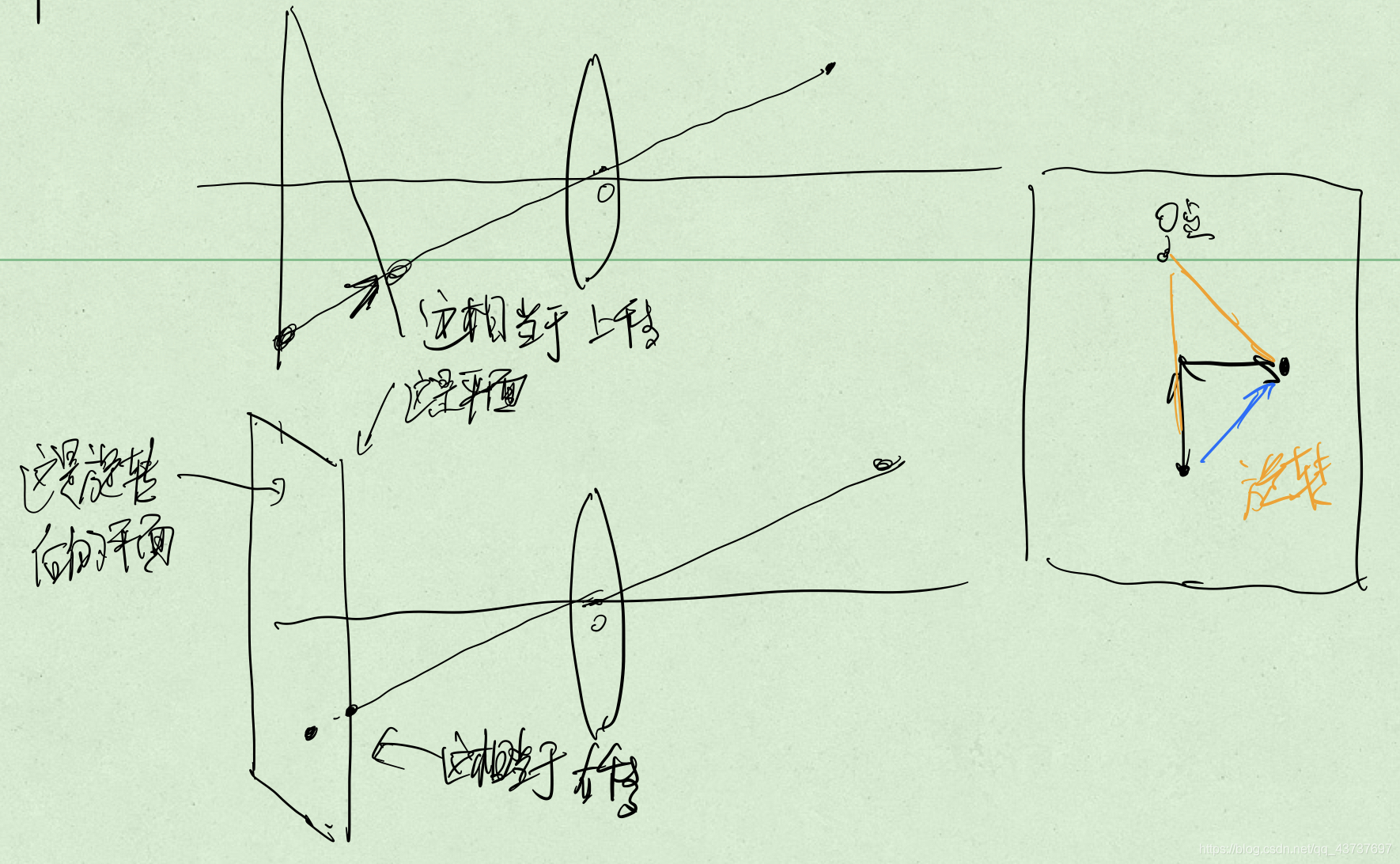
径向畸变

$$ \begin{array}{l}x_{\text {distrred }}=x\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right) \\y_{\text {distorted }}=y\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)\end{array} $$

(xdistorted, ydistorted)是径向畸变后的归一化坐标

切向畸变

$$ \begin{array}{l}x_{\text {distorted }}=x+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right) \\y_{\text {distorred }}=y+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x y\end{array} $$

径向畸变+切向畸变

$$ \left\{\begin{array}{l}x_{\text {distorted }}=x\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)+2 p_{1} x y+p_{2}\left(r^{2}+2 x^{2}\right) \\y_{\text {distorted }}=y\left(1+k_{1} r^{2}+k_{2} r^{4}+k_{3} r^{6}\right)+p_{1}\left(r^{2}+2 y^{2}\right)+2 p_{2} x y\end{array}\right. $$

实际可灵活保留各项系数

投影到像素平面

$$ \left\{\begin{array}{l}u=f_{x} x_{\text {distorted }}+c_{x} \\v=f_{y} y_{\text {distorted }}+c_{y}\end{array}\right. $$

去畸变（undistort）的方式有两种，对整张图去畸变，然后就可以用针孔模型，第二种从畸变图像上的某个点出发，根据畸变方程还原。实际上第一种更好用。

总结

双目相机模型

由于用了归一化平面（z=1），所以散失了深度，怎么求像素平面上每个像素的深度？

用双目相机

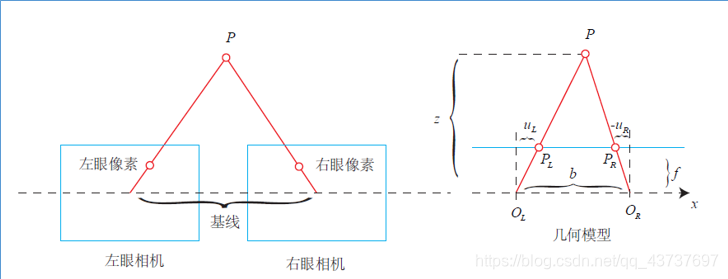
$$ \frac{z-f}{z}=\frac{b-u_{L}+u_{R}}{b} $$

$$ z=\frac{f b}{d}, \quad d=u_{L}-u_{R} $$

UR是负数，b是基线，d是视差

视差d的计算很难，需要知道左边像素点在右边图像中对应哪个。由于计算量，双目深度的估计仍需要使用cpu和fpga

RGB-D模型

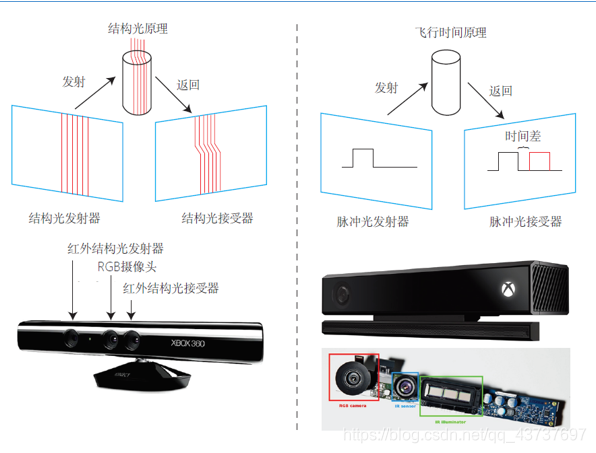
红外结构光原理 structured light ：发射光线，根据返回的结构光图案判断

飞行时间原理 time-of-flight ToF ：发射光线，接收，计算时间差

像素的深度信息形成点云（point cloud）

RGB-D相机的缺点：红外光容易受到日光或其他传感器发射的红外光干扰，不能在室外使用。同时使用多个RGB-D会互相干扰，透射材质的物体难以反射红外光。

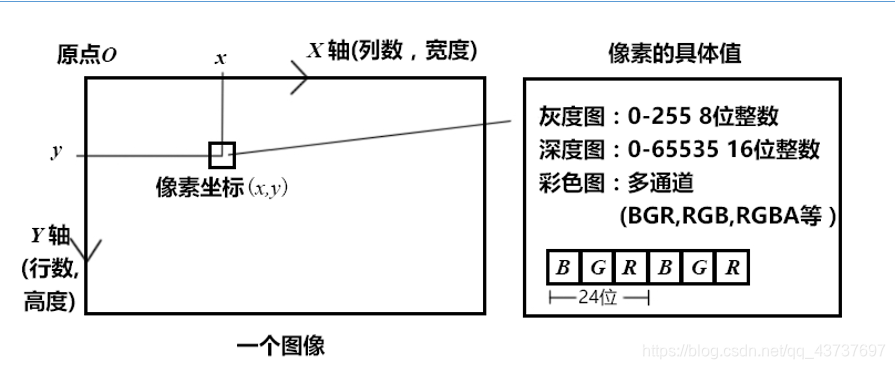
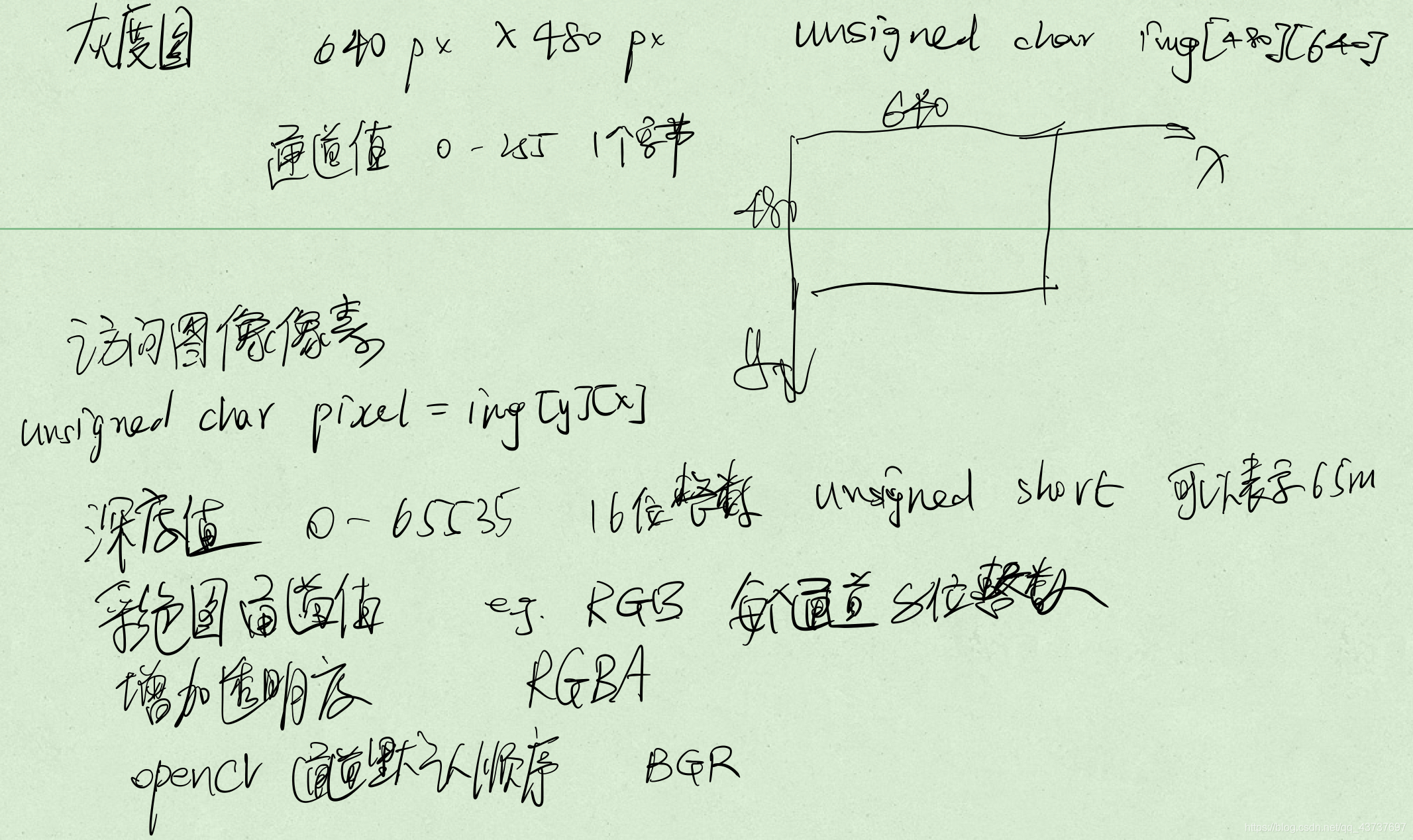
图像

计算机如何处理图像？