非线性优化
相关知识
主要是对高数、概率论、线性代数、数值计算方法、数学建模的一些复习和补充
矩阵求导
全概率公式
$$ P(B)=\sum_{i=1}^{n} P\left(A_{i}\right) P\left(B \mid A_{i}\right) $$
贝叶斯公式
$$ P\left(B_{i} \mid A\right)=\frac{P\left(B_{i}\right) P\left(A \mid B_{i}\right)}{\sum_{j=1}^{n} P\left(B_{j}\right) P\left(A \mid B_{j}\right)} $$
先验概率、后验概率、似然概率
已知车祸、酒驾、高峰可能造成堵车
先验概率(prior probability)
人通过直觉知道它的概率或通过实验(大数定律)获得它的概率
此处为P(X=车祸), P(X=酒驾), P(X=高峰)
似然概率(likelihood probability)
指某种原因下出现某种结果的概率
P(Y=堵车|X=车祸) , P(Y=堵车|X=酒驾), P(Y=堵车|X=高峰)
最大似然估计(maximum likelihood estimation)MLE
使似然概率最大的估计
后验概率(posterior probability)
指某种结果下推测由某种原因导致的概率
P(X=车祸|Y=堵车), P(X=酒驾|Y=堵车), P(X=高峰|Y=堵车)
最大后验估计(maximum a posterior estimation)MAP
使后验概率最大的估计
正态分布

数学期望
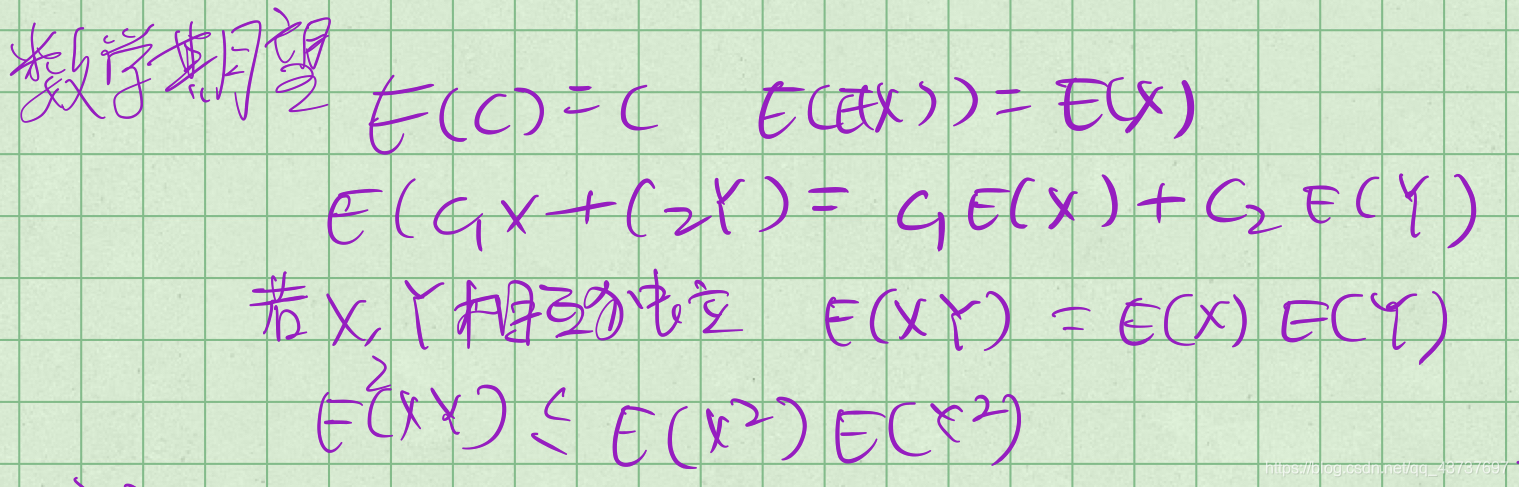
方差
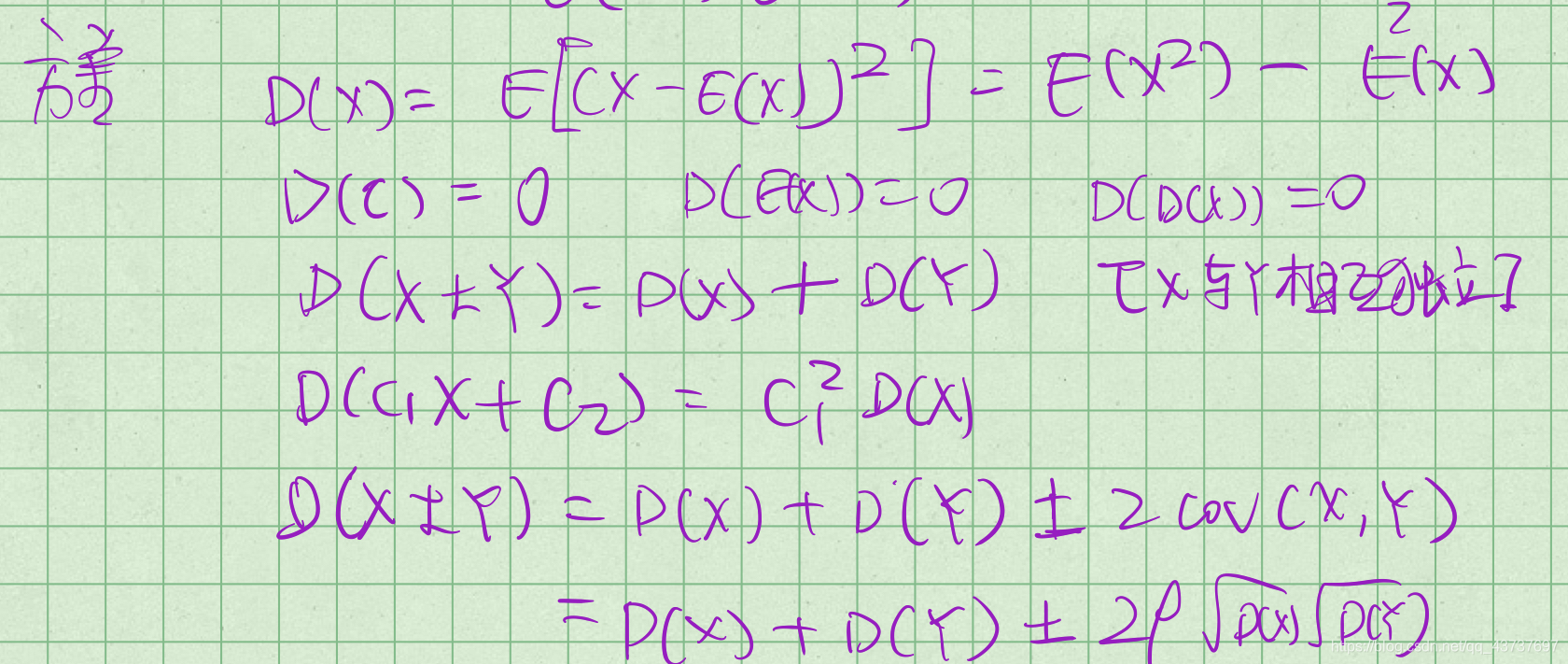
协方差

n维正态分布
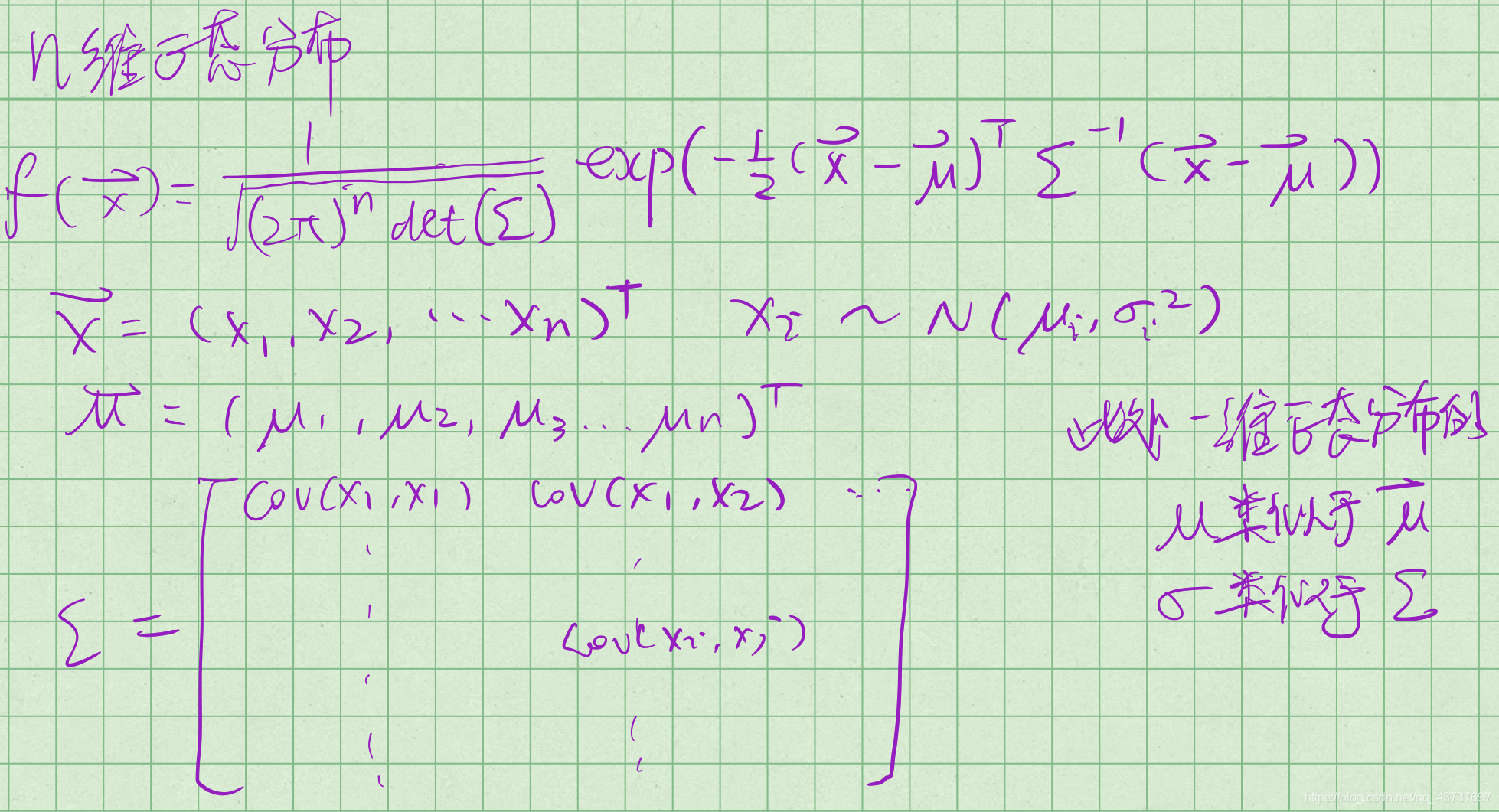
二次型

最小二乘法解超定方程组
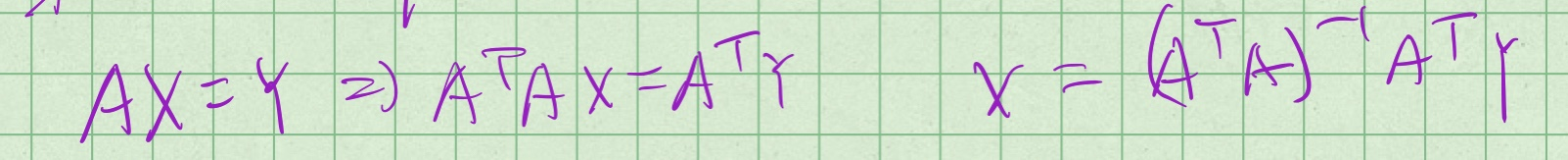
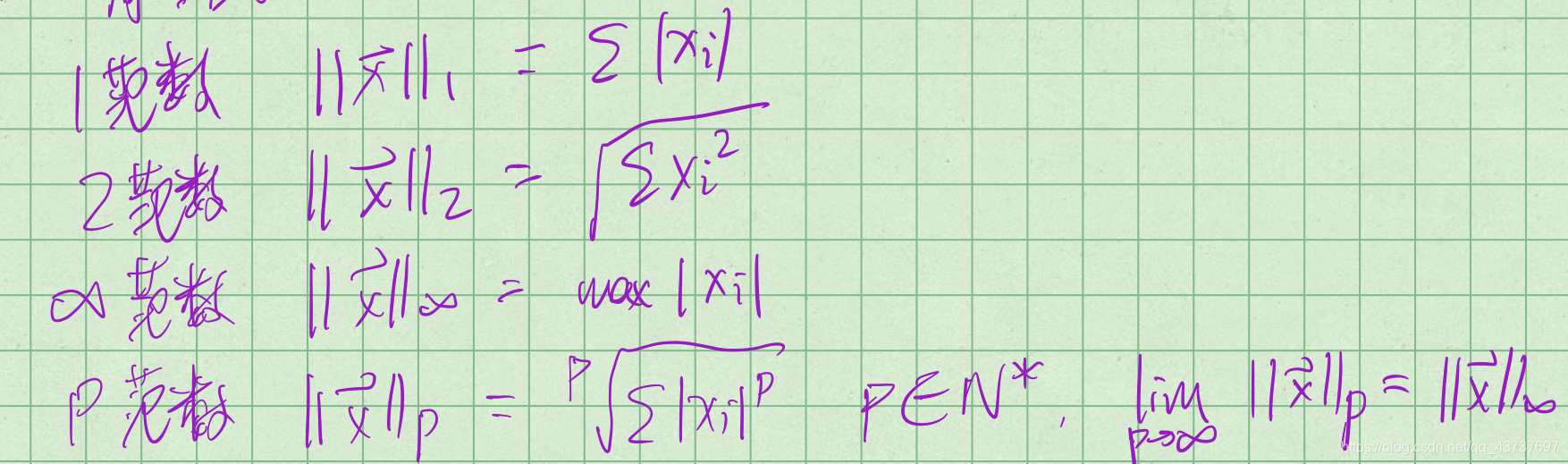
向量的范数
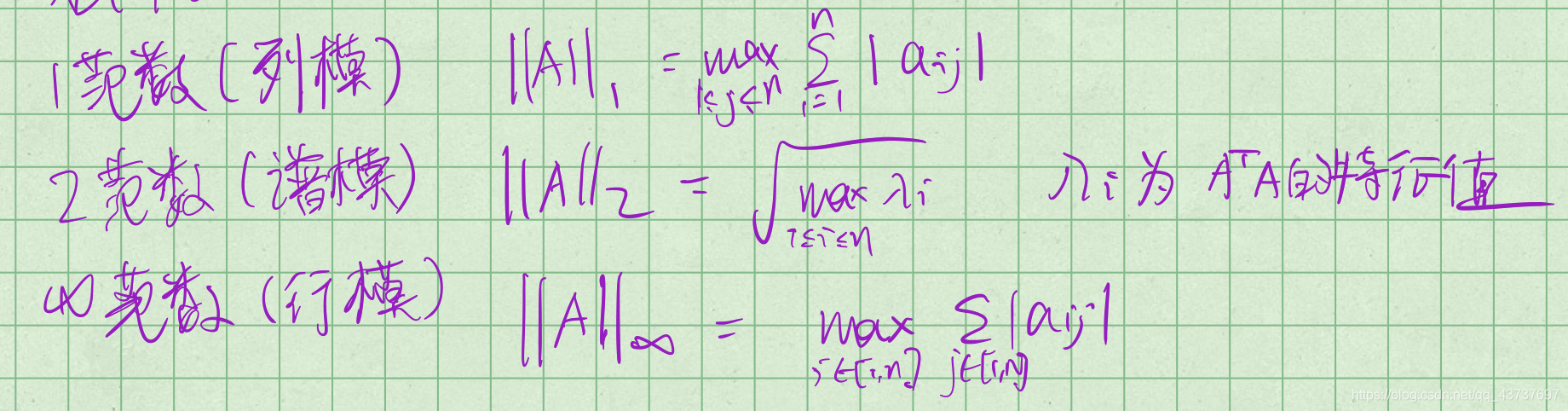
矩阵的范数
求特征值和特征向量

非线性规划算法
无约束非线性规划:梯度下降法,牛顿法,高斯牛顿法
有约束非线性规划:SUMT外点法(罚函数法), SUMT内点法(障碍函数法)
SUMT=sequential unconstrained minimization technique
梯度下降法
gradient descent

牛顿法

状态估计问题
批量状态估计和最大后验估计
考虑经典的slam模型
$$ \left\{\begin{array}{l}\boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}, \boldsymbol{w}_{k}\right) \\\boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}, \boldsymbol{v}_{k, j}\right)\end{array}\right. $$
x是位姿,u是传感器输入,y是路标点,z是产生的观测数据,w,v是噪声
具体地,xk由SE(3)的变换矩阵表示,暂不考虑传感器的输入形式
假设在xk处对路标yj进行了一次观测,对应到图像上的像素位置zk,j,那么观测方程可以表示成
$$ s \boldsymbol{z}_{k, j}=\boldsymbol{K}\left(\boldsymbol{R}_{k} \boldsymbol{y}_{j}+\boldsymbol{t}_{k}\right) $$
K是相机内参,s是像素点的距离,也是(Rkyj+tk)的第三个分量,如果使用变换矩阵Tk描述位姿,yj必须以齐次坐标描述,计算完后转为非齐次
考虑噪声
一般假设wk,vk,j满足μ=0的正态分布
$$ \boldsymbol{w}_{k} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{R}_{k}\right), \boldsymbol{v}_{k} \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{Q}_{k, j}\right) $$
slam的问题变成通过带噪声的z,u来推断位姿x和地图y,这就是状态估计
处理状态估计的方法
incremental 增量/渐近/滤波器 扩展卡尔曼滤波
batch 批量(把数据攒起来,然后处理这段时间的,相当于一段时间一段时间地处理)
batch的方法可以在更大的范围内达到最优,incremental只关心当前
batch方法在视觉slam中更常用,或者将两者结合
考虑1到N的所有时刻,假设有M个路标点
位姿和地图表示为
$$ x=\left\{x_{1}, \ldots, x_{N}\right\}, \quad y=\left\{y_{1}, \ldots, y_{M}\right\} $$
从概率学来看就是求
$$ P(\boldsymbol{x}, \boldsymbol{y}\mid \boldsymbol{z}, \boldsymbol{u}) $$
如果只考虑观测方程(即只有一张张图像),则变成
$$ P(\boldsymbol{x}, \boldsymbol{y}\mid \boldsymbol{z}) $$
此问题也称sfm(structure from motion)即如何从许多图像中重建三维空间结构
根据bayes rule
$$ \underbrace{P(x, y \mid z, u)}_{\text{posterior}}=\frac{P(z, u \mid x, y) P(x, y)}{P(z, u)} \propto \underbrace{P(z, u \mid x, y)}_{\text {likelihood }} \underbrace{P({x},{y})}_{\text {prior }} . $$
直接求后验概率分布是很困难的,但是可以求一个最优估计,由于分母p(z, u)与x,y无关,所以可省略
那么求后验概率就变成
$$ (\boldsymbol{x}, \boldsymbol{y})^{*}{ }_{\mathrm{MAP}}=\arg \max P(\boldsymbol{x}, \boldsymbol{y} \mid \boldsymbol{z}, \boldsymbol{u})=\arg \max P(\boldsymbol{z}, \boldsymbol{u} \mid \boldsymbol{x}, \boldsymbol{y}) P(\boldsymbol{x}, \boldsymbol{y}) $$
由上式可知求map就是最大化likelihood和prior的乘积
当不知道位姿和路标大概在什么地方时,就没有了先验
$$ (x, y)_{\text {MAP }}^{*}=\arg \max P(z, u \mid x, y)=(x, y)_{\text {MLE }}^{*} $$
这就变成了直接求最大似然估计
最小二乘
观测方程
$$ \boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}\right)+\boldsymbol{v}_{k, j} $$
噪声服从正态分布
$$ \boldsymbol{v}_{k} \sim N\left(0, \boldsymbol{Q}_{k, j}\right) $$
所以概率也服从正态分布
$$ P\left(\boldsymbol{z}_{j, k} \mid \boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)=N\left(h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}\right), \boldsymbol{Q}_{k, j}\right) $$
考虑单次观测的MLE,使用最小化负对数求正态分布的MLE
$$ P(\boldsymbol{x})=\frac{1}{\sqrt{(2 \pi)^{N} \operatorname{det}(\boldsymbol{\Sigma})}} \exp \left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right) $$
$$ -\ln (P(\boldsymbol{x}))=\frac{1}{2} \ln \left((2 \pi)^{N} \operatorname{det}(\boldsymbol{\Sigma})\right)+ \frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{T} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}) $$
问题变成
$$ \begin{aligned}\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)^{*} &=\arg \max \mathcal{N}\left(h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}\right), \boldsymbol{Q}_{k, j}\right) \\&=\arg \min \left(\left(\boldsymbol{z}_{k, j}-h\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)\right)^{\mathrm{T}} \boldsymbol{Q}_{k, j}^{-1}\left(\boldsymbol{z}_{k, j}-h\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)\right)\right)\end{aligned} $$
这是一个二次型,这个二次型称为马哈拉诺比斯距离(mahalanobis distance),又叫马氏距离,(Qi,j)-1为信息矩阵
考虑批处理,输入和观测、输入和输入、观测和观测之间互相独立
$$ P(z, u \mid x, y)=\prod_{k} P\left(u_{k} \mid x_{k-1}, x_{k}\right) \prod_{k, j} P\left(z_{k, j} \mid x_{k}, y_{j}\right) $$
这说明z和u可以单独处理
定义误差
$$ \begin{aligned}e_{u, k} &=\boldsymbol{x}_{k}-f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right) \\\boldsymbol{e}_{\boldsymbol{z}, j, k} &=\boldsymbol{z}_{k, j}-h\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)\end{aligned} $$
本来的问题是
$$ \begin{aligned}\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)^{*} &=\arg \min \left(\left(\boldsymbol{z}_{k, j}-h\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)\right)^{\mathrm{T}} \boldsymbol{Q}_{k, j}^{-1}\left(\boldsymbol{z}_{k, j}-h\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)\right)\right)\end{aligned} $$
因为加了批处理,问题变成了
$$ \sum\left(\boldsymbol{x}_{k}, \boldsymbol{y}_{j}\right)^{*} $$
$$ \min J(\boldsymbol{x}, \boldsymbol{y})=\sum_{k} e_{\boldsymbol{u}, k}^{\mathrm{T}} \boldsymbol{R}_{k}^{-1} \boldsymbol{e}_{\boldsymbol{u}, k}+\sum_{k} \sum_{j} \boldsymbol{e}_{\boldsymbol{z}, k, j}^{\mathrm{T}} \boldsymbol{Q}_{k, j}^{-1} \boldsymbol{e}_{\boldsymbol{z}, k, j} $$
这可以看成是最小二乘问题,解等价于MLE
批量状态估计例子
假设运动方程和观测方程是
$$ \begin{array}{ll}\boldsymbol{x}_{k}=\boldsymbol{x}_{k-1}+\boldsymbol{u}_{k}+\boldsymbol{w}_{k}, & \boldsymbol{w}_{k} \sim \mathcal{N}\left(0, \boldsymbol{Q}_{k}\right) \\\boldsymbol{z}_{k}=\boldsymbol{x}_{k}+\boldsymbol{n}_{k}, & \boldsymbol{n}_{k} \sim \mathcal{N}\left(0, \boldsymbol{R}_{k}\right)\end{array} $$
这个式子没有y,y是常量,y是世界坐标系的路标点
这可以表示一辆在x轴上行驶的车
取时间k=1, 2, 3,已知u,y,x0(初始状态),进行状态估计
位姿
$$ x=\left[x_{0}, x_{1}, x_{2}, x_{3}\right]^{\mathrm{T}} $$
观测
$$ z=\left[ z_{1}, z_{2}, z_{3}\right]^{\mathrm{T}} $$
传感器输入
$$ u=\left[ u_{1}, u_{2}, u_{3}\right]^{\mathrm{T}} $$
由之前的推导知
$$ \begin{aligned}x_{\text {map }}^{*} &=\arg \max P(\boldsymbol{x} \mid \boldsymbol{u}, \boldsymbol{z})=\arg \max P(\boldsymbol{u}, \boldsymbol{z} \mid \boldsymbol{x}) \\&=\prod_{k=1}^{3} P\left(\boldsymbol{u}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{k}\right) \prod_{k=1}^{3} P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right)\end{aligned} $$
$$ P\left(\boldsymbol{u}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{k}\right)=\mathcal{N}\left(\boldsymbol{x}_{k}-\boldsymbol{x}_{k-1}, \boldsymbol{Q}_{k}\right) $$
$$ P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right)=\mathcal{N}\left(\boldsymbol{x}_{k}, \boldsymbol{R}_{k}\right) $$
$$ \boldsymbol{e}_{\boldsymbol{u}, k}=\boldsymbol{x}_{k}-\boldsymbol{x}_{k-1}-\boldsymbol{u}_{k}, \quad \boldsymbol{e}_{z, k}=\boldsymbol{z}_{k}-\boldsymbol{x}_{k}, $$
最小二乘的目标函数
$$ \min \sum_{k=1}^{3} e_{u, k}^{\mathrm{T}} \boldsymbol{Q}_{k}^{-1} e_{\boldsymbol{u}, k}+\sum_{k=1}^{3} \boldsymbol{e}_{\boldsymbol{z}, k}^{\mathrm{T}} \boldsymbol{R}_{k}^{-1} \boldsymbol{e}_{z, k} $$
定义向量
$$ \boldsymbol{y}=[\boldsymbol{u}, \boldsymbol{z}]^{\mathrm{T}} $$
$$ y-\boldsymbol{H} \boldsymbol{x}=\boldsymbol{e} \sim \mathcal{N}(\mathbf{0}, \mathbf{\Sigma}) $$
$$ \boldsymbol{H}=\left[\begin{array}{cccc}1 & -1 & 0 & 0 \\0 & 1 & -1 & 0 \\0 & 0 & 1 & -1 \\0 & 1 & 0 & 0 \\0 & 0 & 1 & 0 \\0 & 0 & 0 & 1\end{array}\right] $$
$$ \Sigma=\operatorname{diag}\left(Q_{1}, Q_{2}, Q_{3}, R_{1}, R_{2}, R_{3}\right) $$
整个问题可以写成
$$ \boldsymbol{x}_{\text {map }}^{*}=\arg \min \boldsymbol{e}^{\mathrm{T}} \boldsymbol{\Sigma}^{-1} \boldsymbol{e} $$
$$ \boldsymbol{x}_{\text {map }}^{*}=\left(\boldsymbol{H}^{\mathrm{T}} \boldsymbol{\Sigma}^{-1} \boldsymbol{H}\right)^{-1} \boldsymbol{H}^{\mathrm{T}} \boldsymbol{\Sigma}^{-1} \boldsymbol{y} $$
这个公式只针对例子
非线性最小二乘
考虑这个问题
$$ \min _{x} \frac{1}{2}\|f(x)\|_{2}^{2} $$
x是n维向量
一般直观的求法是dF/dx=0,当dF/dx不好求时用迭代法
梯度下降法
见相关知识部分
牛顿法
见相关知识部分
高斯牛顿法
最速下降法和牛顿法虽然直观,但实用当中存在一些缺点
最速下降法会碰到zigzag问题(过于贪婪)
牛顿法迭代次数少,但需要计算复杂的Hessian矩阵
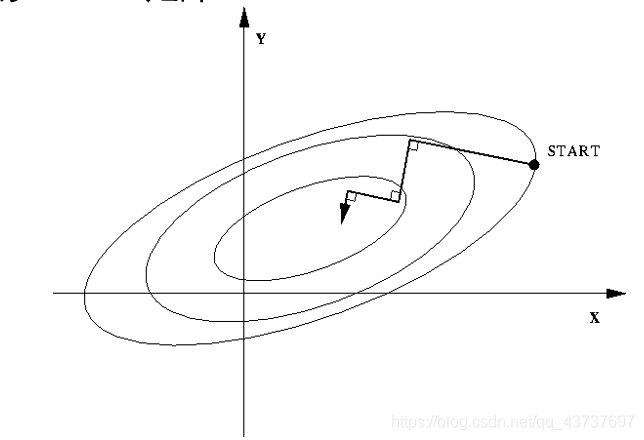
能否回避Hessian的计算?
guass-newton
将f(x)进行一阶的泰勒展开(注意x是n维向量)
$$ f(\boldsymbol{x}+\Delta \boldsymbol{x}) \approx f(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \Delta \boldsymbol{x} $$
J(x)是否转置都可以,取决于求导用的分子布局还是分母布局,不过一般要统一并且灵活应用
J(x)T类似于df(x)/dx,是n*1的列向量,J(x)是Jacobi矩阵
寻找Δx,使得 $\|f(\boldsymbol{x}+\Delta \boldsymbol{x})\|^{2}$ 最小
$$\Delta \boldsymbol{x}^{*}=\arg \min _{\Delta \boldsymbol{x}} \frac{1}{2}\left\|f(\boldsymbol{x})+\boldsymbol{J}(\boldsymbol{x})^{\mathrm{T}} \Delta \boldsymbol{x}\right\|^{2}$$
1/2是系数,加与不加无所谓
$$\begin{aligned}\frac{1}{2}\left\|f(x)+J(x)^{\mathrm{T}} \Delta x\right\|^{2} &=\frac{1}{2}\left(f(x)+J(x)^{\mathrm{T}} \Delta x\right)^{\mathrm{T}}\left(f(x)+J(x)^{\mathrm{T}} \Delta x\right) \\&=\frac{1}{2}\left(\|f(x)\|_{2}^{2}+2 f(x) J(x)^{\mathrm{T}} \Delta x+\Delta x^{\mathrm{T}} J(x) J(x)^{\mathrm{T}} \Delta x\right) \end{aligned}$$
求上式对于Δx的导数,并令其为0
$$J(x) f(x)+J(x) J^{\top}(x) \Delta x=0$$
$$\underbrace{\boldsymbol{J}(\boldsymbol{x}) \boldsymbol{J}^{\mathrm{T}}}_{\boldsymbol{H}(\boldsymbol{x})}(\boldsymbol{x}) \Delta \boldsymbol{x}=\underbrace{-\boldsymbol{J}(\boldsymbol{x}) f(\boldsymbol{x})}_{\boldsymbol{g}(\boldsymbol{x})} $$
$$H \Delta x=g$$
在牛顿法中
$$\nabla f\left(x^{(k)}\right)+H\left(x^{(k)}\right)\left(x-x^{(k)}\right)=0$$
$$J+H\Delta x = 0$$
GN法就是用JJT代替H
GN法的迭代步骤如下
- 给定初值$x_0$
- 对于第k次迭代,求$J(x_k)$和误差$f(x_k)$ (因为$H\Delta x=g$中需要)
- 求增量方程 $H \Delta x_k = g$
- 若$\Delta x_k$ 足够小,则停止,否则$x_{k+1}=x_k+\Delta x$,跳2
可以看出主要是求$H\Delta x=g$中的$\Delta x$

有些GN法的变种为
$$(\Delta \boldsymbol{x}, \alpha)^{*}=\arg \min \left\| f(x+\alpha \Delta x) \right\|^{2}$$
求完Δx后求α
列文伯格-马夸尔特法
levenberg-marquadt
GN法只能在展开点附近有较好的近似效果,LM法一定程度上修正了GN法的缺点,收敛速度比GN法慢
LM法给Δx加一个范围,称为信赖域(trust region),这个范围定义了什么情况下近似是有效的,这类方法也叫信赖域法(trust region method)
用ρ来刻画近似好坏程度
$$\rho=\frac{f(x+\Delta x)-f(x)}{J(x)^{T} \Delta x}$$
再次声明J的转置取决于求导用的分子布局还是分母布局,其实没有差别
这个式子的分子是实际情况,分母是近似情况
ρ接近1,近似效果好,太小,缩小近似范围,太大,扩大近似范围
所以对GN法改造后的LM法如下
- 给初值$x_0$和初始优化半径μ
- 对于第k次迭代,在GN法上增加trust region求解,μ是信赖域半径,D是系数矩阵 $$ \min _{\Delta \boldsymbol{x}_{k}} \frac{1}{2}\left\|f\left(\boldsymbol{x}_{k}\right)+\boldsymbol{J}\left(\boldsymbol{x}_{k}\right)^{T} \Delta \boldsymbol{x}_{k}\right\|^{2}, \quad \text { s.t. }\left\|\boldsymbol{D} \Delta \boldsymbol{x}_{k}\right\|^{2} \leq \mu $$
- 根据它,计算ρ $$\rho=\frac{f(x+\Delta x)-f(x)}{J(x)^{T} \Delta x}$$
- 若ρ>3/4, μ=2μ
- 若ρ<1/4,μ=0.5μ
- 若μ大于某阈值,则认为近似可行,$x_{k+1}=x_k+\Delta x$
- 判断算法是否收敛,不收敛跳2,否则结束
近似范围扩大的倍数和阈值都是可调的
对于 $\left\|\boldsymbol{D} \Delta \boldsymbol{x}_{k}\right\|^{2} \leq \mu$ 可以认为Δx限定在半径为μ的球中,带上D之后变成椭球
列文伯格说D取I(单位阵),马夸尔特说D取非负数对角阵(实际通常用$J^TJ$的对角元素平方根,使得在梯度小的维度上约束范围大一点)
对于这个带约束的非线性优化,可用拉格朗日乘数法解(Lagrange Multiplier Method)(另一种方法是罚函数法)
$$\mathcal{L}\left(\Delta \boldsymbol{x}_{k}, \lambda\right)=\frac{1}{2}\left\|f\left(\boldsymbol{x}_{k}\right)+\boldsymbol{J}\left(\boldsymbol{x}_{k}\right)^{\mathrm{T}} \Delta \boldsymbol{x}_{k}\right\|^{2}+\frac{\lambda}{2}\left(\left\|\boldsymbol{D} \Delta \boldsymbol{x}_{k}\right\|^{2}-\mu\right)$$
和GN法一样,令
$$\frac{d\mathcal{L}\left(\Delta \boldsymbol{x}_{k}, \lambda\right)}{d\Delta x_k}=0$$
$$\left(\boldsymbol{H}+\lambda \boldsymbol{D}^{\mathrm{T}} \boldsymbol{D}\right) \Delta \boldsymbol{x}_{k}=\boldsymbol{g}$$
假设D=I
$$(\boldsymbol{H}+\lambda \boldsymbol{I}) \Delta \boldsymbol{x}_{k}=\boldsymbol{g}$$

总结:初值很重要