Kalman Filter in One Dimension
卡尔曼滤波就是用测量值(measured value)、测量不确定度(measurement uncertainty)、估计值(estimated value)、估计不确定度(estimate uncertainty),通过一轮轮的迭代来使估计值接近真实值(true value)。需要初始化测量值和估计不确定度。
迭代的过程可以分成状态更新(state update)和预测(prediction)
算法流程和方程
以下方程是针对某个特定场景,比如汽车行驶
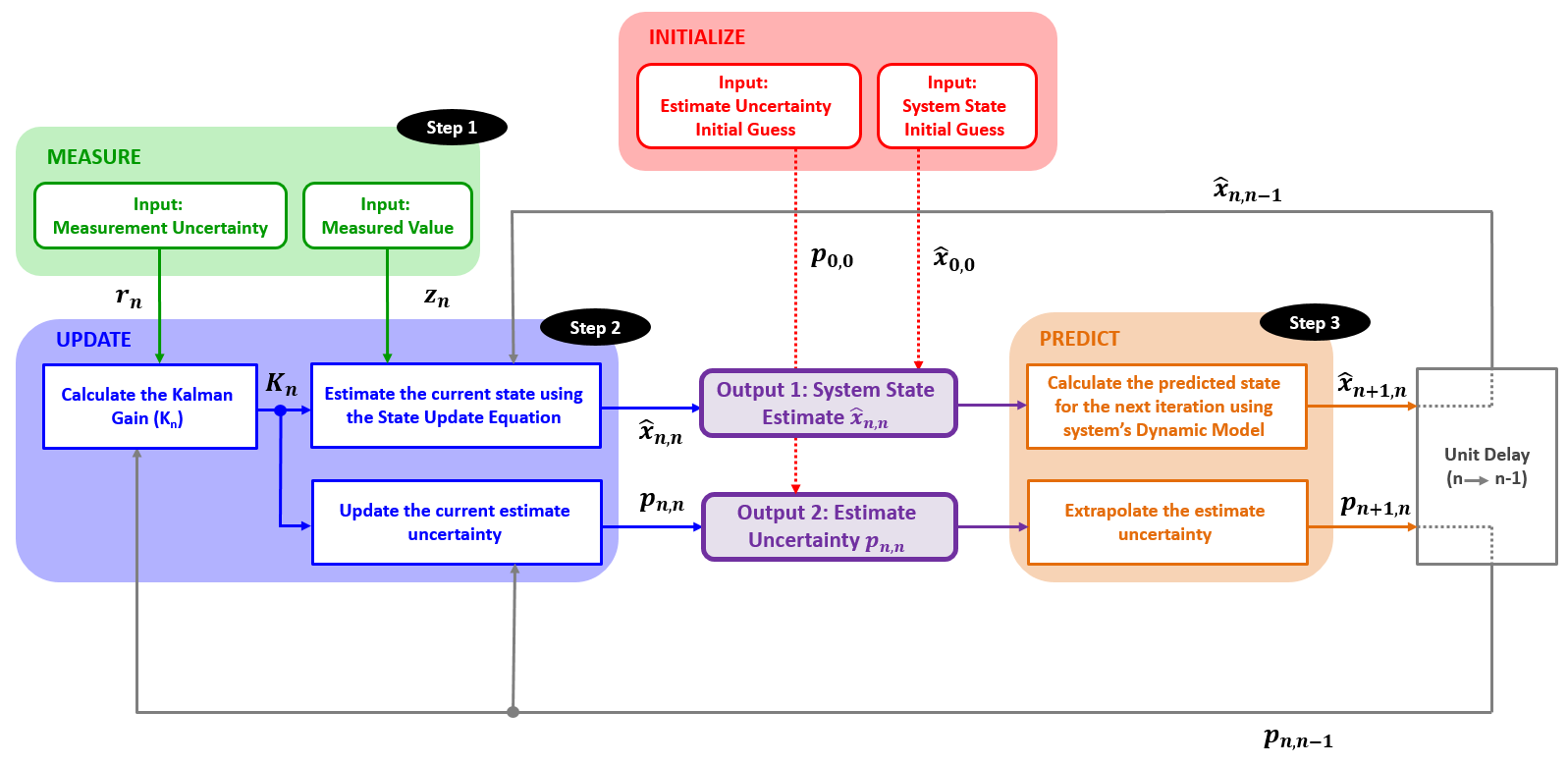
| Equation | Equation Name |
|---|---|
| $$\hat{x}_{n, n}=\hat{x}_{n, n-1}+K_{n}\left(z_{n}-\hat{x}_{n, n-1}\right)$$ | State Update |
| $$\begin{array}{l}\hat{x}_{n+1, n}=\hat{x}_{n, n}+\Delta t \hat{v}_{n, n} \\ \hat{v}_{n+1, n}=\hat{v}_{n, n}\end{array}$$ (For constant velocity dynamics) | State Extrapolation |
| $$K_{n}=\frac{p_{n, n-1}}{p_{n, n-1}+r_{n}}$$ | Kalman Gain |
| $$p_{n, n}=\left(1-K_{n}\right) p_{n, n-1}$$ | Covariance Update |
| $$p_{n+1, n}=p_{n, n}+q_n$$(For constant dynamics) | Covariance Extrapolation |
参数说明
下标为n,n-1意思是第n-1到第n轮,一般为第n-1轮的输出即第n轮的输入
下标为n,n为第n轮的过渡变量,即状态更新了,还没预测
| Parameter | Meaning |
|---|---|
| $$\hat{x}$$ | System State Estimate (Position) |
| $$K$$ | Kalman Gain |
| $$z$$ | Measured Value |
| $$\hat{v}$$ | System State Estimate (Velocity) |
| $$p$$ | Estimate Uncertainty |
| $$r$$ | Measurement Uncertainty |
| $$q$$ | Noise |
卡尔曼增益的数学含义
A low measurement uncertainty relative to the estimate uncertainty would result in a high Kalman Gain (close to 1). Therefore the new estimate would be close to the measurement.
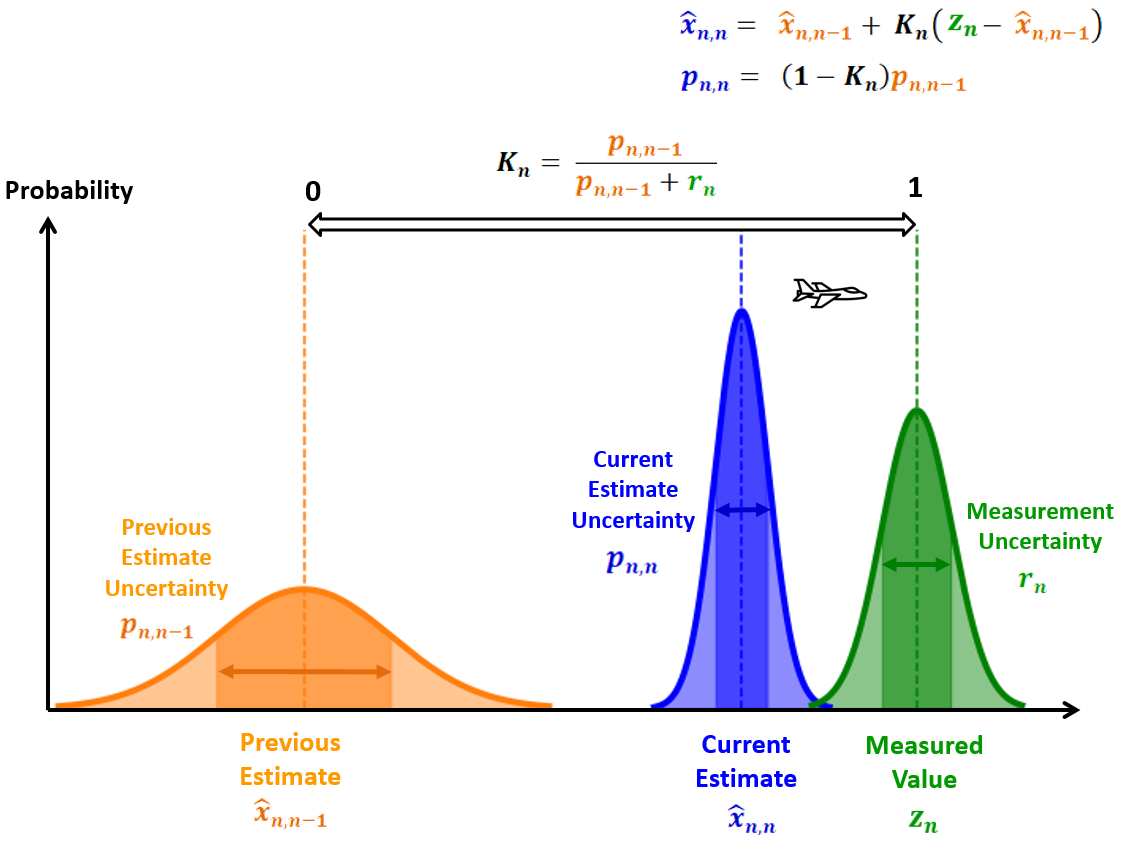
A high measurement uncertainty relative to the estimate uncertainty would result in a low Kalman Gain (close to 0). Therefore the new estimate would be close to the previous estimate.
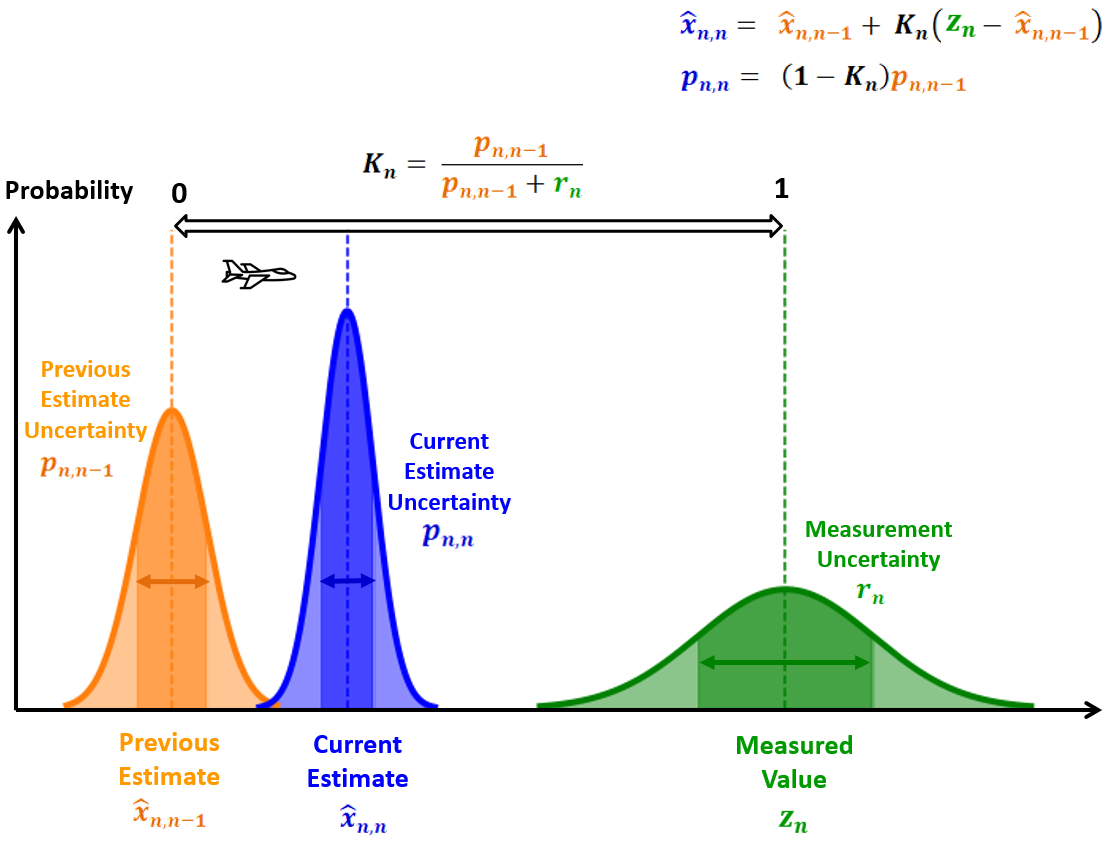
例子参见原文
有时当测量的物体在变化时,卡尔曼滤波不准,可以通过改进模型使它更贴近真实情况或增大噪音
We can eliminate the lag error by setting a high process uncertainty. However, since our model is not well-defined, we get noisy estimates that are almost equal to the measurements, and we miss the goal of the Kalman Filter. The best Kalman Filter implementation would involve a model that is very close to reality, leaving little room for process noise. However, a precise model is not always available - for example, an airplane pilot may decide to perform a sudden maneuver that changes the predicted airplane trajectory. In this case, the process noise would be increased.