VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator

简要记录一下论文的内容，防止遗忘，有些地方自己也没弄明白，记录不涉及公式的推导（公式推导参考崔华坤vins公式推导）

Abstract

VINS-Mono是一个由港科大秦通、栗培梁、沈劭劼完成的单目VI状态估计器，输入相机的图片和IMU参数，经过非线性优化，实时输出位姿和地图。

代码在此链接

Introduction

由于单目相机对尺度不可测，所以使用IMU辅助。单目VIO系统存在一些问题，比如为了成功初始化需要有足够的加速度激励。由于系统高度非线性，初始化也比较麻烦。外参标定和误差漂移也是问题。所以作者提出了VINS-Mono。

作者提出本文的主要贡献为

• 鲁棒的初始化
• 紧耦合和基于优化的VIO可以进行外参标定和IMU偏置估计
• 在线回环检测和紧耦合的重定位
• 四自由度全局位姿图优化
• 实际应用良好
• 开源

Related Work

有关视觉里程计的算法有很多，PTAM、SVO、LSD-SLAM、DSO、ORB-SLAM。最简单的VIO是IMU和视觉松耦合的EKF，紧耦合的VIO既可以使用滤波（常用MSCKF），也可以使用优化（批图优化和BA配合滑窗）。

对于视觉测量的处理，一般有直接法和特征点法。直接法依赖于光度误差，计算量小，对初始位姿估计要求严格。特征点法依赖于平面的几何位移，计算量大，主要体现在提取和匹配特征点上。实际中，由于特征点法更成熟和鲁棒，也更常用，在稠密建图上直接法更好用。

IMU通常有很高的频率，对于优化方法，通常使用IMU预积分。

Overview

VINS的结构图如下

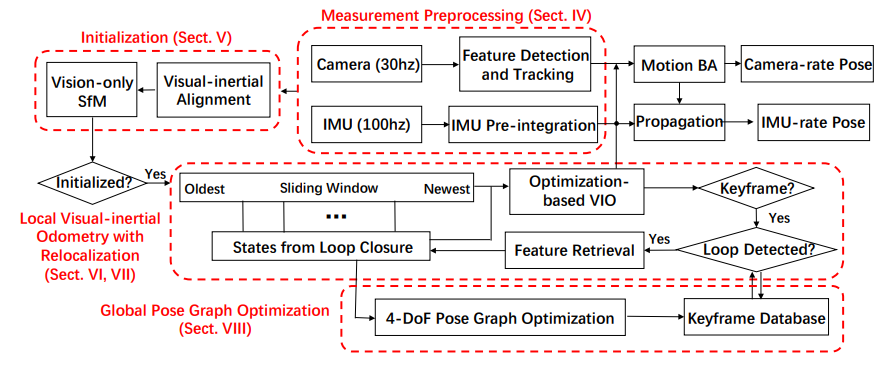
在一开始时，图像会进行特征点追踪和提取，IMU数据进行预积分。在V部分会进行纯视觉SfM和视觉惯性对齐，这部分叫初始化，初始化之后就可以得到必要的信息（每一帧的位姿，速度，重力，陀螺仪偏置，3D点坐标）为后续非线性优化使用。在VI和VII部分，非线性优化将使用紧耦合的视觉和IMU数据，并且使用回环检测进行重定位。最后在VIII部分，使用重定位的结果进行全局位姿图优化，重定位和位姿图优化并行进行。

Measurement Preprocessing

测量预处理包括图像的特征点追踪和提取，IMU的预积分。

Vision Processing Front-end

图像首先进行特征点追踪，然后提取新的角点，使用RANSAC进行外点剔除。

关键帧的判断有两个条件：如果当前帧和上一个关键帧的特征点平均视差过大，当前帧就是关键帧。如果跟踪到的点很少，当前帧就是关键帧。

IMU Pre-integration

一些前置定义

区分两个概念，测量值和真实值，测量值可以直接通过传感器得到，真实值是测量值尽可能消去误差（bias和noise）得到的

下标k是图像帧，下标i是IMU帧

原始的陀螺仪和加速度计的测量值

$$ \begin{aligned} \hat{\mathbf{a}}_{t} & =\mathbf{a}_{t}+\mathbf{b}_{a_{t}}+\mathbf{R}_{w}^{t} \mathbf{g}^{w}+\mathbf{n}_{a} \end{aligned} $$

$$ \begin{aligned} \hat{\boldsymbol{\omega}}_{t} & =\boldsymbol{\omega}_{t}+\mathbf{b}_{w_{t}}+\mathbf{n}_{w} \end{aligned} $$

假设噪声满足正态分布，偏置的导数满足正态分布

第k+1图像帧的位移、速度和旋转（在世界坐标系下）可以通过上一帧得到

$$ \begin{array}{l} \mathbf{p}_{b_{k+1}}^{w}=\mathbf{p}_{b_{k}}^{w}+\mathbf{v}_{b_{k}}^{w} \Delta t_{k} +\iint_{t \in\left[t_{k}, t_{k+1}\right]}\left(\mathbf{R}_{t}^{w}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{a_{t}}-\mathbf{n}_{a}\right)-\mathbf{g}^{w}\right) d t^{2} \end{array} $$

$$ \begin{array}{l} \mathbf{v}_{b_{k+1}}^{w}=\mathbf{v}_{b_{k}}^{w}+\int_{t \in\left[t_{k}, t_{k+1}\right]}\left(\mathbf{R}_{t}^{w}\left(\hat{\mathbf{a}}_{t}-\mathbf{b}_{a_{t}}-\mathbf{n}_{a}\right)-\mathbf{g}^{w}\right) d t \end{array} $$

$$ \begin{array}{l} \mathbf{q}_{b_{k+1}}^{w}=\mathbf{q}_{b_{k}}^{w} \otimes \int_{t \in\left[t_{k}, t_{k+1}\right]} \frac{1}{2} \boldsymbol{\Omega}\left(\hat{\boldsymbol{\omega}}_{t}-\mathbf{b}_{w_{t}}-\mathbf{n}_{w}\right) \mathbf{q}_{t}^{b_{k}} d t \end{array} $$

行内公式:

公式块:

原始的带有 Markdown 语法的内容:

由上面的公式可以看出，Rwt是待优化变量，每次优化调整时，就需要重新传递才能使其他量更准确，很浪费时间，所以采用预积分的策略

不在世界坐标系下求pvq，而是在bk系下求，这样公式转变成

$$ \begin{aligned} \mathbf{R}{w}^{b{k}} \mathbf{p}{b{k+1}}^{w} & =\mathbf{R}{w}^{b{k}}\left(\mathbf{p}{b{k}}^{w}+\mathbf{v}{b{k}}^{w} \Delta t_{k}-\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}\right)+\boldsymbol{\alpha}{b{k+1}}^{b_{k}} \ \mathbf{R}{w}^{b{k}} \mathbf{v}{b{k+1}}^{w} & =\mathbf{R}{w}^{b{k}}\left(\mathbf{v}{b{k}}^{w}-\mathbf{g}^{w} \Delta t_{k}\right)+\boldsymbol{\beta}{b{k+1}}^{b_{k}} \ \mathbf{q}{w}^{b{k}} \otimes \mathbf{q}{b{k+1}}^{w} & =\gamma_{b_{k+1}}^{b_{k}} \end{aligned} $$

$$ \begin{aligned} \boldsymbol{\alpha}{b{k+1}}^{b_{k}} & =\iint_{t \in\left[t_{k}, t_{k+1}\right]} \mathbf{R}{t}^{b{k}}\left(\hat{\mathbf{a}}{t}-\mathbf{b}{a_{t}}-\mathbf{n}{a}\right) d t^{2} \ \boldsymbol{\beta}{b_{k+1}}^{b_{k}} & =\int_{t \in\left[t_{k}, t_{k+1}\right]} \mathbf{R}{t}^{b{k}}\left(\hat{\mathbf{a}}{t}-\mathbf{b}{a_{t}}-\mathbf{n}{a}\right) d t \ \boldsymbol{\gamma}{b_{k+1}}^{b_{k}} & =\int_{t \in\left[t_{k}, t_{k+1}\right]} \frac{1}{2} \boldsymbol{\Omega}\left(\hat{\boldsymbol{\omega}}{t}-\mathbf{b}{w_{t}}-\mathbf{n}{w}\right) \boldsymbol{\gamma}{t}^{b_{k}} d t \end{aligned} $$

三个预积分项可以近似看成是相邻图像帧之间的pvq的变化量，可以看出三个预积分项没有待优化变量。三个预积分项和bias有关，当bias变化时，变化不大，则用预积分项的一阶近似代替，变化很大则重传递

上面的预积分项是连续的，实际是用离散形式代替，离散形式有欧拉法、中点法等，论文写的是欧拉法，代码中用的是中点法。欧拉法的预积分项传递公式如下（不考虑噪声）

$$ \begin{array}{l} \hat{\boldsymbol{\alpha}}{i+1}^{b{k}}=\hat{\boldsymbol{\alpha}}{i}^{b{k}}+\hat{\boldsymbol{\beta}}{i}^{b{k}} \delta t+\frac{1}{2} \mathbf{R}\left(\hat{\gamma}{i}^{b{k}}\right)\left(\hat{\mathbf{a}}{i}-\mathbf{b}{a_{i}}\right) \delta t^{2} \ \hat{\boldsymbol{\beta}}{i+1}^{b{k}}=\hat{\boldsymbol{\beta}}{i}^{b{k}}+\mathbf{R}\left(\hat{\gamma}{i}^{b{k}}\right)\left(\hat{\mathbf{a}}{i}-\mathbf{b}{a_{i}}\right) \delta t \ \hat{\boldsymbol{\gamma}}{i+1}^{b{k}}=\hat{\boldsymbol{\gamma}}{i}^{b{k}} \otimes\left[\begin{array}{c} 1 \ \frac{1}{2}\left(\hat{\boldsymbol{\omega}}{i}-\mathbf{b}{w_{i}}\right) \delta t \end{array}\right] \end{array} $$

预积分和bias的误差传递公式如下

$$ \begin{array}{l} {\left[\begin{array}{c} \delta \dot{\boldsymbol{\alpha}}{t}^{b{k}} \ \delta \dot{\boldsymbol{\beta}}{t}^{b{k}} \ \delta \dot{\boldsymbol{\theta}}{t}^{b{k}} \ \delta \dot{\mathbf{b}}{a{t}} \ \delta \dot{\mathbf{b}}{w{t}} \end{array}\right]=\left[\begin{array}{ccccc} 0 & \mathbf{I} & 0 & 0 & 0 \ 0 & 0 & -\mathbf{R}{t}^{b{k}}\left\lfloor\hat{\mathbf{a}}{t}-\mathbf{b}{a_{t}}\right\rfloor_{\times} & -\mathbf{R}{t}^{b{k}} & 0 \ 0 & 0 & -\left\lfloor\hat{\boldsymbol{\omega}}{t}-\mathbf{b}{w_{t}}\right\rfloor_{\times} & 0 & -\mathbf{I} \ 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 \end{array}\right]\left[\begin{array}{c} \delta \boldsymbol{\alpha}{t}^{b{t}} \ \delta \boldsymbol{\beta}{t}^{b{k}} \ \delta \boldsymbol{\theta}{t}^{b{k}} \ \delta \mathbf{b}{a{t}} \ \delta \mathbf{b}{w{t}} \end{array}\right]} \ +\left[\begin{array}{cccc} 0 & 0 & 0 & 0 \ -\mathbf{R}{t}^{b{k}} & 0 & 0 & 0 \ 0 & -\mathbf{I} & 0 & 0 \ 0 & 0 & \mathbf{I} & 0 \ 0 & 0 & 0 & \mathbf{I} \end{array}\right]\left[\begin{array}{c} \mathbf{n}{a} \ \mathbf{n}{w} \ \mathbf{n}{b{a}} \ \mathbf{n}{b{w}} \end{array}\right]=\mathbf{F}{t} \delta \mathbf{z}{t}^{b_{k}}+\mathbf{G}{t} \mathbf{n}{t} \ \end{array} $$

根据误差传递公式可以获得误差的协方差矩阵和误差（残差）对于待优化变量的雅克比矩阵

协方差矩阵P用于后端非线性优化，雅克比矩阵J用来修正测量值，得到理论上的真实值

$$ \begin{array}{c} \mathbf{P}{t+\delta t}^{b{k}}=\left(\mathbf{I}+\mathbf{F}{t} \delta t\right) \mathbf{P}{t}^{b_{k}}\left(\mathbf{I}+\mathbf{F}{t} \delta t\right)^{T}+\left(\mathbf{G}{t} \delta t\right) \mathbf{Q}\left(\mathbf{G}_{t} \delta t\right)^{T}, \ t \in[k, k+1] \end{array} $$

初始值$P_{b_k}^{b_k}=0$，Q是正态分布的方差$\left(\boldsymbol{\sigma}{a}^{2}, \boldsymbol{\sigma}{w}^{2}, \boldsymbol{\sigma}{b{a}}^{2}, \boldsymbol{\sigma}{b{w}}^{2}\right)$

雅克比矩阵也同样可以迭代地计算

$$ \mathbf{J}{t+\delta t}=\left(\mathbf{I}+\mathbf{F}{t} \delta t\right) \mathbf{J}_{t}, \quad t \in[k, k+1] $$

初始值$J_{b_k}=I$

这样预积分项就可以用一阶泰勒展示来修正

$$ \begin{aligned} \boldsymbol{\alpha}{b{k+1}}^{b_{k}} & \approx \hat{\boldsymbol{\alpha}}{b{k+1}}^{b_{k}}+\mathbf{J}{b{a}}^{\alpha} \delta \mathbf{b}{a{k}}+\mathbf{J}{b{w}}^{\alpha} \delta \mathbf{b}{w{k}} \ \boldsymbol{\beta}{b{k+1}}^{b_{k}} & \approx \hat{\boldsymbol{\beta}}{b{k+1}}^{b_{k}}+\mathbf{J}{b{a}}^{\beta} \delta \mathbf{b}{a{k}}+\mathbf{J}{b{w}}^{\beta} \delta \mathbf{b}{w{k}} \ \boldsymbol{\gamma}{b{k+1}}^{b_{k}} & \approx \hat{\boldsymbol{\gamma}}{b{k+1}}^{b_{k}} \otimes\left[\begin{array}{c} 1 \ \frac{1}{2} \mathbf{J}{b{w}}^{\gamma} \delta \mathbf{b}{w{k}} \end{array}\right] \end{aligned} $$

如果bias有微小的变动也可以用上述公式来修正

最后总结一下预积分的公式如下

$$ \left[\begin{array}{c} \hat{\boldsymbol{\alpha}}{b{k+1}}^{b_{k}} \ \hat{\boldsymbol{\beta}}{b{k+1}}^{b_{k}} \ \hat{\boldsymbol{\gamma}}{b{k+1}}^{b_{k}} \ \mathbf{0} \ \mathbf{0} \end{array}\right]=\left[\begin{array}{c} \mathbf{R}{w}^{b{k}}\left(\mathbf{p}{b{k+1}}^{w}-\mathbf{p}{b{k}}^{w}+\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}-\mathbf{v}{b{k}}^{w} \Delta t_{k}\right) \ \mathbf{R}{w}^{b{k}}\left(\mathbf{v}{b{k+1}}^{w}+\mathbf{g}^{w} \Delta t_{k}-\mathbf{v}{b{k}}^{w}\right) \ \mathbf{q}{b{k}}^{b^{-1}} \otimes \mathbf{q}{b{k+1}}^{w} \ \mathbf{b}{a b{k+1}}-\mathbf{b}{a b{k}} \ \mathbf{b}{w b{k+1}}-\mathbf{b}{w b{k}} \end{array}\right] $$

Estimator Initialization

先纯视觉SfM，然后视觉和IMU对齐恢复尺度、重力、速度、bias。在初始化时，忽略加速度计的bias

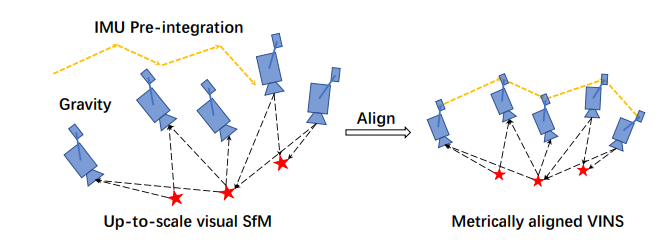
Sliding Window Vision-Only SfM

当滑窗满了开始初始化，求最新帧和前面帧的共视点，如果前面存在一个帧有足够的共视点和视差，则那一帧当做参考帧，通过五点法求出不含尺度的相对旋转和位移。如果找不到参考帧，则移出最老帧，等待新帧。

如果五点法成功，则三角化参考帧和最新帧的共视点。有了3D点，通过PnP求滑窗中其他帧的位姿。最后全局BA

Visual-Inertial Alignment

Gyroscope Bias Calibration

陀螺仪偏置的标定通过最小化如下函数来求，其中q由SfM得到，γ由IMU得到

$$ \begin{array}{r} \min {\delta b{w}} \sum_{k \in \mathcal{B}}\left|\mathbf{q}{b{k+1}}^{c_{0}}{ }^{-1} \otimes \mathbf{q}{b{k}}^{c_{0}} \otimes \boldsymbol{\gamma}{b{k+1}}^{b_{k}}\right|^{2} \ \gamma_{b_{k+1}}^{b_{k}} \approx \hat{\gamma}{b{k+1}}^{b_{k}} \otimes\left[\begin{array}{c} 1 \ \frac{1}{2} \mathbf{J}{b{w}}^{\gamma} \delta \mathbf{b}_{w} \end{array}\right] \end{array} $$

B表示滑窗所有帧

求出陀螺仪偏置后重传递更新所有的IMU预积分

Velocity, Gravity Vector and Metric Scale Initialization

待求的变量为

$$ \mathcal{X}{I}=\left[\mathbf{v}{b_{0}}^{b_{0}}, \mathbf{v}{b{1}}^{b_{1}}, \cdots \mathbf{v}{b{n}}^{b_{n}}, \mathbf{g}^{c_{0}}, s\right] $$

论文中给出了结论，求这个向量就是最小化以下函数

$$ \min {\mathcal{X}{I}} \sum_{k \in \mathcal{B}}\left|\hat{\mathbf{z}}{b{k+1}}^{b_{k}}-\mathbf{H}{b{k+1}}^{b_{k}} \mathcal{X}_{I}\right|^{2} $$

$$ \hat{\mathbf{z}}{b{k+1}}^{b_{k}}=\left[\begin{array}{c} \hat{\boldsymbol{\alpha}}{b{k+1}}^{b_{k}}-\mathbf{p}{c}^{b}+\mathbf{R}{c_{0}}^{b_{k}} \mathbf{R}{b{k+1}}^{c_{0}} \mathbf{p}{c}^{b} \ \hat{\boldsymbol{\beta}}{b_{k+1}}^{b_{k}} \end{array}\right] $$

$$ \mathbf{H}{b{k+1}}^{b_{k}}=\left[\begin{array}{cccc} -\mathbf{I} \Delta t_{k} & \mathbf{0} & \frac{1}{2} \mathbf{R}{c{0}}^{b_{k}} \Delta t_{k}^{2} & \mathbf{R}{c{0}}^{b_{k}}\left(\overline{\mathbf{p}}{c{k+1}}^{c_{0}}-\overline{\mathbf{p}}{c{k}}^{c_{0}}\right) \ -\mathbf{I} & \mathbf{R}{c{0}}^{b_{k}} \mathbf{R}{b{k+1}}^{c_{0}} & \mathbf{R}{c{0}}^{b_{0}} \Delta t_{k} \end{array}\right] $$

Gravity Refinement

由于重力的值通常是已知的，所以只有2自由度，但是我们求出的g有3自由度，所以进行优化

将g写成这种形式$g \cdot \overline{\hat{\mathbf{g}}}+w_{1} \mathbf{b}{1}+w{2} \mathbf{b}_{2}$，其中g是已知的重力值，g\hat\bar是原本重力的单位向量，b1b2是原本重力切平面的正交基，w1w2是权重

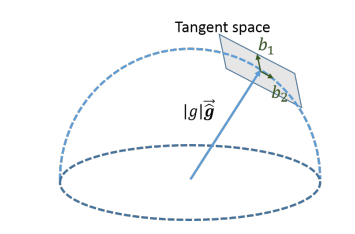b是这样求的

w是通过改写上面公式的H和z求的

Completing Initialization

最后将重力转到z轴，求出一个旋转矩阵，通过旋转矩阵将所有的量从c0系转到世界系

然后这些量将输入进紧耦合VIO中

Tightly-Coupled Monocular VIO

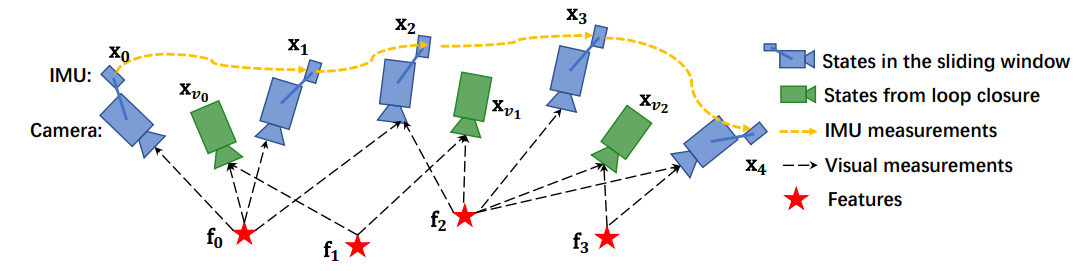
Formulation

待优化变量为滑窗内每个图像pvqb，外参，特征点的逆深度

$$ \begin{aligned} \mathcal{X} & =\left[\mathbf{x}{0}, \mathbf{x}{1}, \cdots \mathbf{x}{n}, \mathbf{x}{c}^{b}, \lambda_{0}, \lambda_{1}, \cdots \lambda_{m}\right] \ \mathbf{x}{k} & =\left[\mathbf{p}{b_{k}}^{w}, \mathbf{v}{b{k}}^{w}, \mathbf{q}{b{k}}^{w}, \mathbf{b}{a}, \mathbf{b}{g}\right], k \in[0, n] \ \mathbf{x}{c}^{b} & =\left[\mathbf{p}{c}^{b}, \mathbf{q}_{c}^{b}\right] \end{aligned} $$

非线性优化的公式如下，这也是VINS最重要的公式，之后会说下公式的含义

$$ \begin{aligned} \min {\mathcal{X}}\left{\left|\mathbf{r}{p}-\mathbf{H}{p} \mathcal{X}\right|^{2}+\right. & \sum{k \in \mathcal{B}}\left|\mathbf{r}{\mathcal{B}}\left(\hat{\mathbf{z}}{b_{k+1}}^{b_{k}}, \mathcal{X}\right)\right|{\mathbf{P}{b_{k+1}}^{b_{k}}}^{2}+ \sum_{(l, j) \in \mathcal{C}} \rho\left(\left|\mathbf{r}{\mathcal{C}}\left(\hat{\mathbf{z}}{l}^{c_{j}}, \mathcal{X}\right)\right|{\left.\mathbf{P}{l}^{c_{j}}\right)}^{2}\right} \end{aligned} $$

这个公式有三项分别是边缘化的先验约束、IMU约束、视觉约束，约束就是残差，其中后两项带有协方差矩阵，最后一项加上Huber核，B是IMU在滑窗内所有的测量值，C是滑窗内被跟踪至少两次的特征点。用ceres solver求解

IMU Measurement Residual

IMU约束是相邻两个图像之间的预积分项的残差

$$ \begin{array}{l} \mathbf{r}{\mathcal{B}}\left(\hat{\mathbf{z}}{b_{k+1}}^{b_{k}}, \mathcal{X}\right)=\left[\begin{array}{c} \delta \boldsymbol{\alpha}{b{k+1}}^{b_{k}} \ \delta \boldsymbol{\beta}{b{k+1}}^{b_{k}} \ \delta \boldsymbol{\theta}{b{k+1}}^{b_{k}} \ \delta \mathbf{b}{a} \ \delta \mathbf{b}{g} \end{array}\right] \ =\left[\begin{array}{c} \mathbf{R}{w}^{b{k}}\left(\mathbf{p}{b{k+1}}^{w}-\mathbf{p}{b{k}}^{w}+\frac{1}{2} \mathbf{g}^{w} \Delta t_{k}^{2}-\mathbf{v}{b{k}}^{w} \Delta t_{k}\right)-\hat{\boldsymbol{\alpha}}{b{k+1}}^{b_{k}} \ \mathbf{R}{w}^{b{k}}\left(\mathbf{v}{b{k+1}}^{w}+\mathbf{g}^{w} \Delta t_{k}-\mathbf{v}{b{k}}^{w}\right)-\hat{\boldsymbol{\beta}}{b{k+1}}^{b_{k}} \ 2\left[\mathbf{q}{b{k}}^{w^{-1}} \otimes \mathbf{q}{b{k+1}}^{w} \otimes\left(\hat{\gamma}{b{k+1}}^{b_{k}}\right)^{-1}\right]{x y z} \ \mathbf{b}{a b_{k+1}}-\mathbf{b}{a b{k}} \ \mathbf{b}{w b{k+1}}-\mathbf{b}{w b{k}} \end{array}\right] \end{array} $$

Visual Measurement Residual

视觉的约束就是重投影误差

误差的距离不是在成像平面上计算，是将特征点像素坐标通过内参投影到单位球上，然后在单位球上求向量的差，因为误差是2维（像素坐标是2维）的，所以误差实际上在单位球的正切平面上算

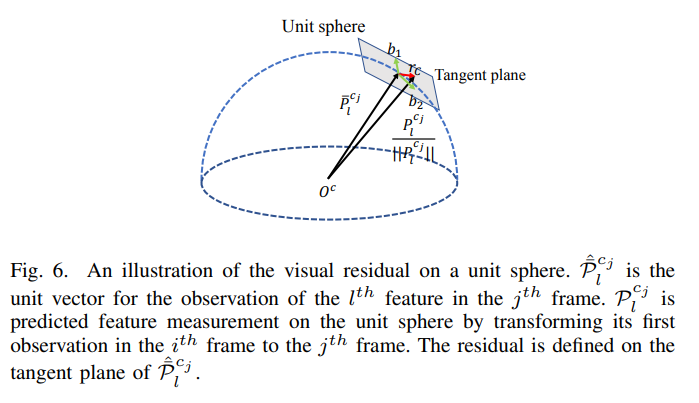
$$ \begin{array}{l} \mathbf{r}{\mathcal{C}}\left(\hat{\mathbf{z}}{l}^{c_{j}}, \mathcal{X}\right)=\left[\begin{array}{ll} \mathbf{b}{1} & \mathbf{b}{2} \end{array}\right]^{T} \cdot\left(\hat{\overline{\mathcal{P}}}{l}^{c{j}}-\frac{\mathcal{P}{l}^{c{j}}}{\left|\mathcal{P}{l}^{c{j}}\right|}\right) \ \begin{array}{l} \hat{\mathcal{P}}{l}^{c{j}}=\pi_{c}{ }^{-1}\left(\left[\begin{array}{c} \hat{u}{l}^{c{j}} \ \hat{v}{l}^{c{j}} \end{array}\right]\right) \ \mathcal{P}{l}^{c{j}}=\mathbf{R}{b}^{c}\left(\mathbf { R } _ { w } ^ { b _ { j } } \left(\mathbf { R } _ { b _ { i } } ^ { w } \left(\mathbf{R}{c}^{b} \frac{1}{\lambda_{l}} \pi_{c}{ }^{-1}\left(\left[\begin{array}{c} u_{l}^{c_{i}} \ v_{l}^{c_{i}} \end{array}\right]\right)\right.\right.\right. \left.\left.\left.+\mathbf{p}{c}^{b}\right)+\mathbf{p}{b_{i}}^{w}-\mathbf{p}{b{j}}^{w}\right)-\mathbf{p}_{c}^{b}\right) \end{array} \end{array} $$

Marginalization

由于要滑窗容量有限，当新帧来时，就需要把滑窗内的某一帧移出去，而移出去的过程就叫边缘化，移出去的帧和相关的数据不能直接丢弃，会作为先验信息加入到非线性优化中

边缘化的策略是，如果次新帧是关键帧，则边缘化最老帧，把相关的VI数据作为先验，如果次新帧不是关键帧，则抛弃它，视觉数据直接抛弃，IMU数据和后面的连在一起

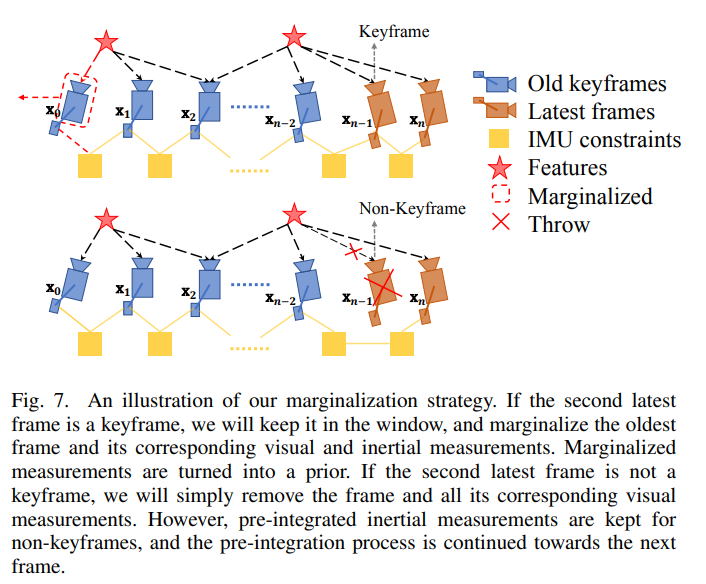
边缘化采用舒尔补，具体形式论文没有详细叙述，详细公式在A General Optimization-based Framework for Local Odometry Estimation with Multiple Sensors论文中叙述

边缘化对导致线性化点的过早固定，这样可能会得到次优解，不过作者认为小误差漂移是可以接受的（可能后续可以通过回环检测来消除）

Motion-only Visual-Inertial Bundle Adjustment for Camera-Rate State Estimation

对于算力不是很足的设备，在优化时只优化后面几帧的数据，而不是整个滑窗的数据

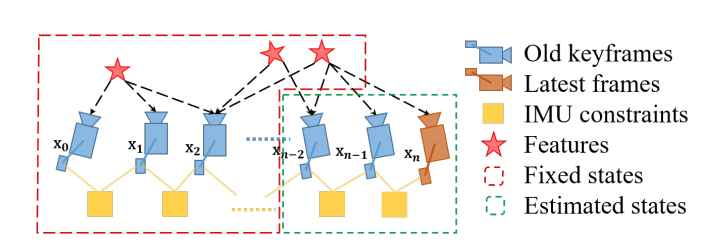
IMU Forward Propagation for IMU-Rate State Estimation

Failure Detection and Recovery

故障检测的标准是：最新帧跟踪的特征点小于某个阈值，估计器输出的最后两帧的位移和旋转差很大，估计器估计的bias和外参在两个时刻差很大

当检测到故障时，回到初始化阶段

Relocalization

由于滑窗和边缘化计算的是局部的信息，会带来误差并累积，所以使用回环检测和重定位来消除

Loop Detection

使用DBoW2词袋模型进行回环检测，除了用于VIO的角点，会额外提取500个角点并计算BRIEF描述子，描述子作为单词进行查找，查找后会返回回环候选帧。我们只保留描述子用于信息检索，原始图像将会被抛弃来减少内存消耗

Feature Retrieval

对于回环候选帧，如果直接比较描述子鲁棒性不是很高

所以先用RANSAC做一次2D-2D的测试，再用RANSAC做一次PnP测试，如果内点大于阈值则为回环帧，然后进行重定位

Tightly-Coupled Relocalization

重定位就是改变非线性优化的代价函数，再加一项视觉的回环约束，因为我们将VIO中这些特征点和回环中看到的这些特征点认为是相同的。但是把从位姿图中拿出的回环帧的位姿保持恒定

如果滑窗有多个回环帧时，一起优化以提高精度和平滑度

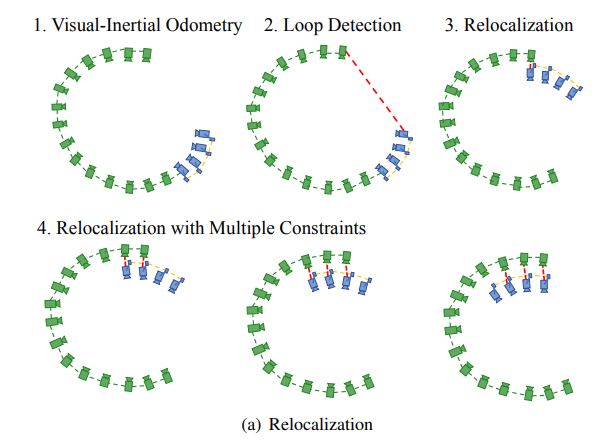
$$ \begin{array}{l} \min {\mathcal{X}}\left{\left|\mathbf{r}{p}-\mathbf{H}{p} \mathcal{X}\right|^{2}+\sum{k \in \mathcal{B}}\left|\mathbf{r}{\mathcal{B}}\left(\hat{\mathbf{z}}{b_{k+1}}^{b_{k}}, \mathcal{X}\right)\right|{\mathbf{P}{b_{k+1}}^{b_{k}}}^{2}\right. +\sum_{(l, j) \in \mathcal{C}} \rho\left(\left|\mathbf{r}{\mathcal{C}}\left(\hat{\mathbf{z}}{l}^{c_{j}}, \mathcal{X}\right)\right|{\mathbf{P}{l}^{c_{j}}}^{2}\right) +\sum_{(l, v) \in \mathcal{L}} \rho\left(\left|\mathbf{r}{\mathcal{C}}\left(\hat{\mathbf{z}}{l}^{v}, \mathcal{X}, \hat{\mathbf{q}}{v}^{w}, \hat{\mathbf{p}}{v}^{w}\right)\right|{\mathbf{P}{l}^{c_{v}}}^{2}\right} \end{array} $$

其中v表示回环帧

Global Pose Graph Optimization

为了使全局保持同步，所以将重定位的结果加进全局位姿图优化中。因为重力方向已经确定，所以三个方向的平移和对重力方向的旋转是不可观的，只进行4自由度的位姿图优化

Adding Keyframes into the Pose Graph

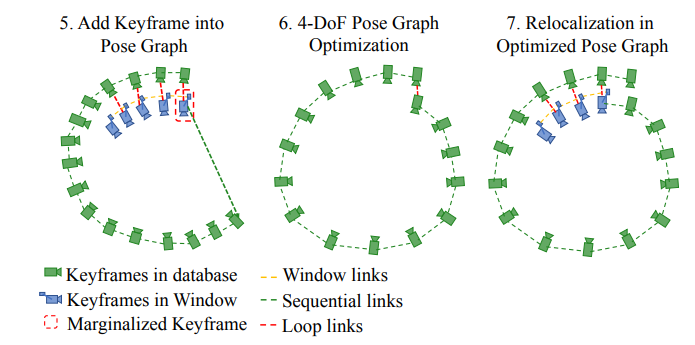
当关键帧从滑窗中边缘化掉后，它将作为顶点加进位姿图中

这个顶点与别的顶点有两种边

序列边：这个关键帧与前面的关键帧相连，边表示的是相对平移，假设刚被边缘化的关键帧i和之前某一个关键帧j，考虑4自由度，平移和yaw角

$$ \begin{aligned} \hat{\mathbf{p}}{i j}^{i} & =\hat{\mathbf{R}}{i}^{w-1}\left(\hat{\mathbf{p}}{j}^{w}-\hat{\mathbf{p}}{i}^{w}\right) \ \hat{\psi}{i j} & =\hat{\psi}{j}-\hat{\psi}_{i} \end{aligned} $$

回环边：如果刚被边缘化的关键帧有回环帧，则加一条4自由度的边，边的值从重定位中获取，形式和上面的公式一样

4-DOF Pose Graph Optimization

定义两帧i和j的残差

$$ \mathbf{r}{i, j}\left(\mathbf{p}{i}^{w}, \psi_{i}, \mathbf{p}{j}^{w}, \psi{j}\right)=\left[\begin{array}{c} \mathbf{R}\left(\hat{\phi}{i}, \hat{\theta}{i}, \psi_{i}\right)^{-1}\left(\mathbf{p}{j}^{w}-\mathbf{p}{i}^{w}\right)-\hat{\mathbf{p}}{i j}^{i} \ \psi{j}-\psi_{i}-\hat{\psi}_{i j} \end{array}\right] $$

全局图的代价函数为

$$ \min {\mathbf{p}, \psi}\left{\sum{(i, j) \in \mathcal{S}}\left|\mathbf{r}{i, j}\right|^{2}+\sum{(i, j) \in \mathcal{L}} \rho\left(\left|\mathbf{r}_{i, j}\right|^{2}\right)\right} $$

其中S是序列边，L是回环边，序列边不加鲁棒核是因为它的数据从VIO中获得，已经进行了外点剔除，具有鲁棒性了

重定位和全局位姿图优化在不同的线程中进行，这样可以保证它们互相使用最新的结果

Pose Graph Management

由于全局位姿图会不断膨胀，在计算上会越来越耗时，所以之后有回环的关键帧会被保留，那些很相似的关键帧将被丢弃